R

使用ArchR分析单细胞ATAC-seq数据(第一章)

第1章: ArchR基础入门

这一章将会介绍如何导入数据，如何构建Arrow文件，这是后续ArchR分析的基础。

1.1 ATAC-seq术语介绍

“fragment“是ATAC-seq实验中的一个重要概念，它指的是通过Tn5转座酶对DNA分子进行酶切，然后经由双端测序得到的序列。

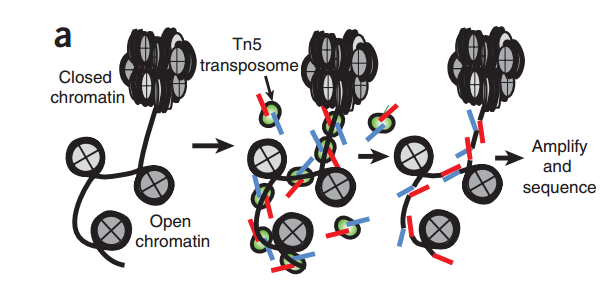
fragment产生过程

我们会根据Tn5插入导致的偏移从read比对得到的位置推断出fragment的起始和结束位置。根据之前的报道，Tn5转座酶以同源二聚体的形式结合到DNA上，在两个Tn5分子间隔着9-bp的DNA序列。根据这个情况，每个Tn5同源二聚体的结合事件会产生2个Insertions，中间隔着9bp。因此，真实的”开放”位置的中心在Tn5二聚体的正中间，而不是Tn5的插入位置。为了尽可能的还原真实情况，我们对Tn5的Insertions进行了校正，即正链的插入结果往右移动4bp(+4 bp), 负链的插入结果往左偏移5bp(-5 bp)。这个和最早提出的ATAC-seq里的描述是一致的。因此，在ArchR中，”fragment“指的是一个table或genomic ranges对象, 记录在染色体上，经过偏移校正后的单碱基起始位置，以及经过偏移校正后单碱基结束位置，每个fragment都会对应唯一的细胞条形码。类似的，”Insertions”这得是偏移校正后的单碱基位置，它位于开放位置的正中心。

“fragment”和”insertions”这两个词我并没有将其翻译成中文，我觉得这两个单词可能就和PCR一样，当说到它们的时候，脑中会有一个画面描述它们，而不是局限一个词。

1.2 为什么是用ArchR

现在其实已经有一些工具能够处理单细胞ATAC-seq数据，我们为什么要额外造一个轮子，开发一个新的项目呢？主要是ArchR提供了其他工具目前尚不能实现的功能

工具对比

不仅如此，ArchR通过优化数据结构降低了内存消耗，使用并行提高了运行速度，因此保证其性能优于其他同类型工具。在超过70,000个细胞的分析项目中，一些软件需要超过128G的可用内存。

性能对比

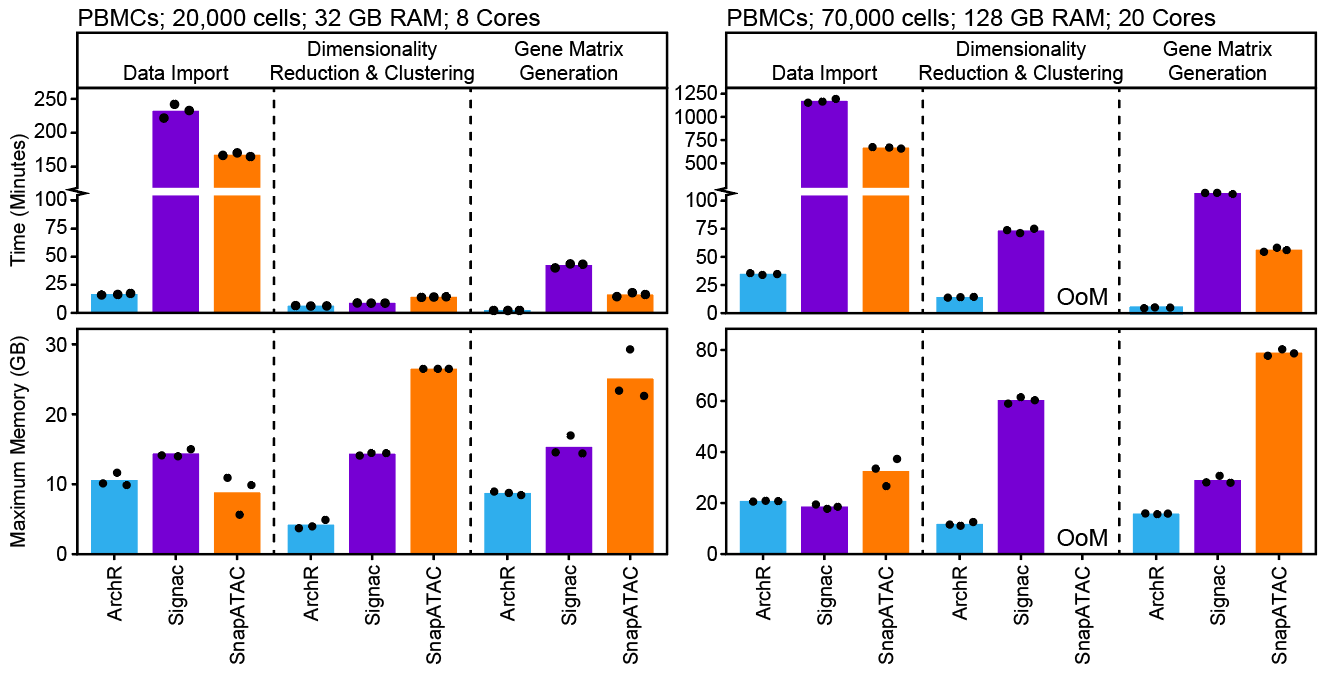
ArchR最初就是根据Unix的笔记本进行设计（我觉得他说的是MacBook Pro），因此对于中等大小的实验（小于100,000个细胞），ArchR能够保证一些特殊分析的运行速度，并能实时的展示结果，让我们能够更深入的和数据进行互动，给出有意义的生物学解释。当然，如果细胞数更多，你最好使用服务器进行分析。ArchR提供了方便的图形导出功能，在服务器处理完项目之后，可以直接下载到本地进行使用。

目前，ArchR并没有针对Windows进行优化。这句话的意思是指，ArchR的并行策略是基于Unix系统而非Windows系统，因此上述说的性能提升不包括Windows。

1.3 什么是Arrow文件/ArchRProject

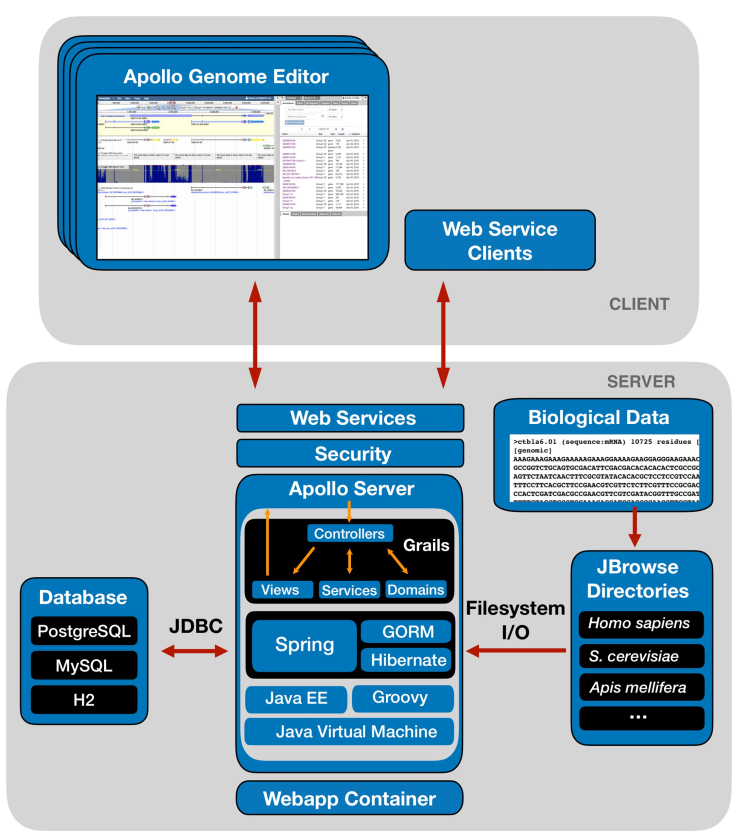
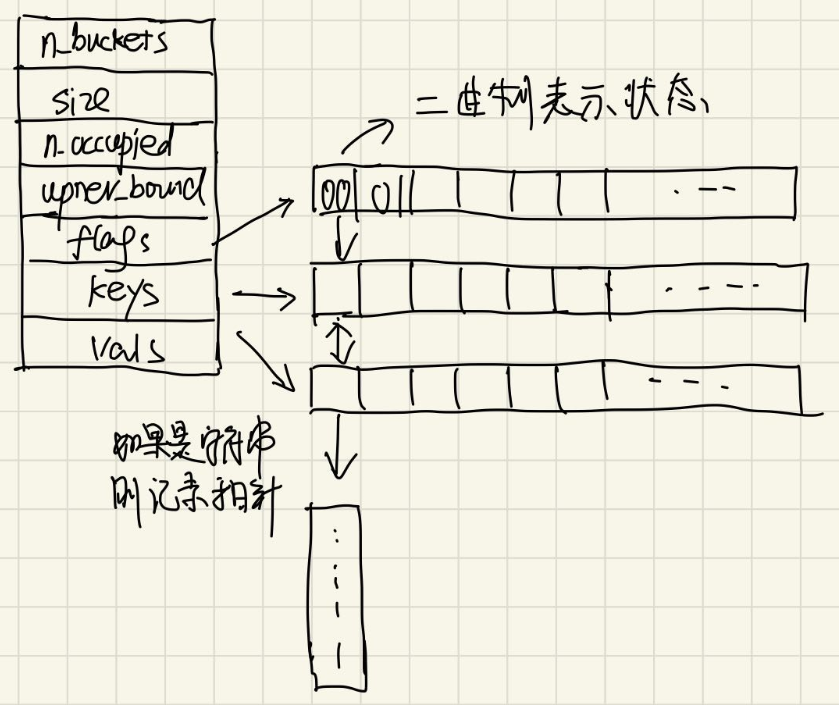
正如开头所说，ArchR分析项目的基础是Arrow文件。每个Arrow文件记录着每个独立样本的所有相关信息（例如元信息、开放的fragment和数据矩阵）。这里说的独立样本最好是最详尽的分析单元（例如，一种特定条件下的单个重复）。在创建Arrow文件以及一些附加分析中，ArchR会编辑和更新相应的Arrow文件，在其中添加额外的信息层。值得注意的是，Arrow文件实际指的是磁盘上的文件路径。更确切的说，Arrow文件并不是一个存放在内存中的R语言对象，而是存放在磁盘上HDF5文件。正因如此，我们使用ArchRProject对象用来关联这些Arrow文件，将其关联到单个分析框架中，从而保证在R中能高效访问它们。而这个ArchRProject对象占用内存不多，因此才是存放在内存中的R语言对象。

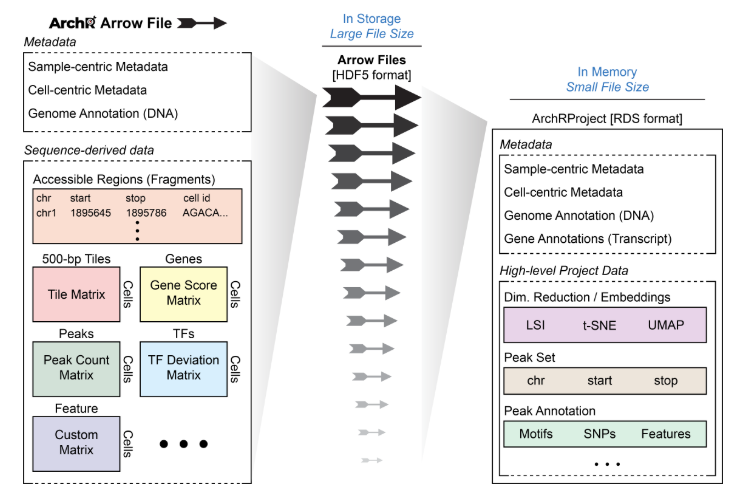
Arrow File

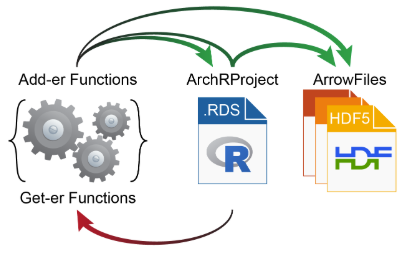
有一些操作会直接修改Arrow文件，而一些操作会先作用于ArchRproject，接着反过来更新每个相关Arrow文件。因为Arrow文件是以非常大的HDF5格式存放，所以ArchR的get-er函数通过和ArchRProject进行交互获取数据，而add-er函数既能直接在Arrow文件中添加数据，也能直接在ArchRpoject里添加数据，或者通过ArchRpoject向Arrow文件添加数据。

ArchRProject

1.4 ArchR的输入文件类型

ArchR主要以scATAC-seq原始数据经上游处理后的两种常见输出文件(BAM, fragment)作为输入。Fragment文件记录着scATAC-seq的fragment以及对应的细胞ID，每一行都是一条记录，该文件需要是tabix(见注1)排序并建立索引保证能被高效读取。BAM文件则是二进制格式下的tabix排序文件，记录着scATAC-seq的fragment、原始数据、细胞条形码和其他信息。具体使用何种文件作为输入取决于你的上游处理流程。以10XGenomics的CellRanger软件为例，它的输出文件是fragments，而sci-ATAC-seq流程则输出BAM文件。

ArchR使用scanTabix函数读取fragment文件，使用scanBAM读取BAM文件。输入过程并不会直接读取所有数据，而是每次读取一大块(chunks)，然后将这一块数据转换成fragment格式(见注2)，经过压缩先暂时以HDF5格式保存到本地磁盘上，避免消耗过多的内存。最后，等所有数据都加载完成之后，该数据相关的所有临时HDF5文件会被重新读取，经过组织之后以单个HDF5形式保存为Arrow文件。ArchR之所以能以较小的内存量高效地读取大文件，就是因为它采用的是这种分块处理的方法，由于每一块数据的处理都互不干扰，因此也就能够并行计算。

  • 注1: 当以制表符记录基因组位置信息时，我们可以通过压缩让其体积变小(bgzip/gzip)，通过建立tabix索引高效访问给定位置的信息。
  • 注2: fragments一共有5列，分别是chromosome, offset-adjusted chromosome start position, offset-adjusted chromosome end position, and cellular barcode ID, duplicate count

1.5 开始设置

在后续分析之前，请先设置好我们的工作目录，设置将要使用的线程数，加载我们的基因和基因组注释。由于每个人的环境都不太一样，所以你后续可能需要用addArchRThreads()修改线程数。默认情况下，ArchR使用系统一半的可用线程，你可以手动进行调整。如果你用的是Windows，那么默认都是1，这是因为ArchR的多线程是基于Unix操作系统。

第零步，安装ArchR。目前ArchR托管在GitHub上，因此无法直接用CRAN或者Bioconductor中直接下载安装。

方法1：适用于网络状态好的情况

1
2
3
if (!requireNamespace("devtools", quietly = TRUE)) install.packages("devtools")
if (!requireNamespace("BiocManager", quietly = TRUE)) install.packages("BiocManager")
devtools::install_github("GreenleafLab/ArchR", ref="master", repos = BiocManager::repositories())

方法2: 适用于上述方法多次失败的情况

先从Github上下载项目到本地, 大约有262Mb

1
git clone https://github.com/GreenleafLab/ArchR.git

然后在 R里面进行安装

1
2
BiocManager::install(c("nabor","motifmatchr","chromVAR","ComplexHeatmap"))
install.packages("./ArchR", repo=NULL)

接着安装一些额外包

1
ArchR::installExtraPackages()

如果安装失败，就手动安装 Seurat, immunogenomics/harmony, immunogenomics/presto, Cairo，shiny, shinythemes, rhandsontable

第一步，我们加载ArchR包。

1
library(ArchR)

第二步, 我们需要设置ArchR函数的默认线程数。你需要在每个新的R session中都设置该参数，线程多多益善，但是不要超过总线程的3/4。因为线程会和内存挂钩，所以线程数越多，内存相应使用的也越多。

1
addArchRThreads(threads = 16)

第三步: 我们设置需要使用基因和基因组注释。同样，这也是每个新的R session需要设置的参数。当然，我们需要使用和序列比对阶段相同的基因组版本。对于本教程使用的数据，我们会使用hg19参考基因组。ArchR支持多种基因组注释，并且允许自定义基因组注释。

1
addArchRGenome("hg19")

基因和基因组注释信息是后续计算TSS富集得分，核小体含量和基因活跃度得分所必需的。同样，你得保证这里选择的基因组版本得和你上游数据处理时用到的基因组版本一致。我们这里设置”hg19”就是因为上数据处理用的是hg19作为参考基因组。除了hg19外，ArchR还提供了”hg38”, “mm9”, “mm10”, 并且允许用户使用createGeneAnnotation和createGenomeAnnotation函数创建其他物种注释。

我们使用addArchRGenome函数无缝地为ArchR提供这些信息。该函数告诉ArchR，在之后的所有分析中，它应该使用定义在ArchRgenome的相关genomeAnnotation和geneAnnotation。每一个原生支持的基因组都包括四个对象(object)

  • BSgenome: 记录 染色体坐标信息和染色体序列信息
  • GRanges: 记录blacklist, 即对分析没有用设置可能产生干扰的区域
  • TxDb: 定义所有基因的位置信息
  • OrgDb: 提供基因编号，以及不同基因编号之间的转换

如下是ArchR自带的物种注释的数据来源

ArchR的预编译的hg19基因组用的是BSgenome.Hsapiens.UCSC.hg19, TxDb.Hsapiens.UCSC.hg19.knownGene, org.Hs.eg.db。而黑名单(记录着一直打开的区域，对后续分析没有帮助的位置）则来源于 hg19 v2 blacklist regions 和mitochondrial regions that show high mappability to the hg19 nuclear genome from Caleb Lareau and Jason Buenrostro，用ArchR::mergeGR()函数进行合并

ArchR的预编译的hg38基因组用的是BSgenome.Hsapiens.UCSC.hg38, TxDb.Hsapiens.UCSC.hg38.knownGene, org.Hs.eg.db。而黑名单(记录着一直打开的区域，对后续分析没有帮助的位置）则来源于 hg19 v2 blacklist regions 和mitochondrial regions that show high mappability to the hg38 nuclear genome from Caleb Lareau and Jason Buenrostro，用ArchR::mergeGR()函数进行合并

ArchR的预编译的mm9基因组用的是BSgenome.Mmusculus.UCSC.mm9, TxDb.Mmusculus.UCSC.mm9.knownGene, org.Mm.eg.db。而黑名单(记录着一直打开的区域，对后续分析没有帮助的位置）则来源于 mm9 v1 blacklist regions 和mitochondrial regions that show high mappability to the mm9 nuclear genome from Caleb Lareau and Jason Buenrostro，用ArchR::mergeGR()函数进行合并

ArchR的预编译的mm10基因组用的是BSgenome.Mmusculus.UCSC.mm10, TxDb.Mmusculus.UCSC.mm10.knownGene, org.Mm.eg.db。而黑名单(记录着一直打开的区域，对后续分析没有帮助的位置）则来源于 mm10 v2 blacklist regions 和mitochondrial regions that show high mappability to the mm10 nuclear genome from Caleb Lareau and Jason Buenrostro，用ArchR::mergeGR()函数进行合并

1.5.1: 自定义ArchRGenome

如上所述，一个ArchRGenome需要包括基因组注释和基因注释

为了构建自定义的基因组注释，我们会使用createGenomeAnnotation. 他需要如下2个信息

  • BSgenome: 包括基因组的序列信息，你可以通过谷歌查找指定物种的Bioconductor包
  • GRanges: 记录基因组中的黑名单区域，用来过滤下游分析中不需要的区间。这不是必须的，毕竟不是所有物种都能有这个文件。 publication on the ENCODE blacklists提供黑名单列表的制作方法。

例如，我们如果需要为Drosophila melanogaster创建一个基因组注释，那么我们需要先下载对应的BSgenome

1
2
3
4
if (!requireNamespace("BSgenome.Dmelanogaster.UCSC.dm6", quietly = TRUE)){
  BiocManager::install("BSgenome.Dmelanogaster.UCSC.dm6")
}
library(BSgenome.Dmelanogaster.UCSC.dm6)

接着，我们从BSgenome对象中创建基因组注释

1
genomeAnnotation <- createGenomeAnnotation(genome = BSgenome.Dmelanogaster.UCSC.dm6)

查看这个对象，你可以看到一个ArchR基因组注释的组成内容

1
2
3
genomeAnnotation
## List of length 3
## names(3): genome chromSizes blacklist

为了构造一个自定义基因注释，我们需要用到createGeneAnnotation()，它需要你提供如下两个信息

  • TxDb: 记录gene/transcript的坐标信息
  • OrgDb: 用于基因名和其他基因编号的转换

继续之前的Drosophila melanogaster案例，我们需要先安装并加载相关的TxDb和OrgDb对象

1
2
3
4
5
6
7
8
if (!requireNamespace("TxDb.Dmelanogaster.UCSC.dm6.ensGene", quietly = TRUE)){
  BiocManager::install("TxDb.Dmelanogaster.UCSC.dm6.ensGene")
}
if (!requireNamespace("org.Dm.eg.db", quietly = TRUE)){
  BiocManager::install("org.Dm.eg.db")
}
library(TxDb.Dmelanogaster.UCSC.dm6.ensGene)
library(org.Dm.eg.db)

记着，我们构建基因注释对象

1
geneAnnotation <- createGeneAnnotation(TxDb = TxDb.Dmelanogaster.UCSC.dm6.ensGene, OrgDb = org.Dm.eg.db)

检查该对象，可以了解ArchR关于基因注释的存放形式

1
2
3
geneAnnotation
## List of length 3
## names(3): genes exons TSS

如果你没有TxDb和OrgDb对象，你也可以直接根据如下信息创建geneAnnotation对象

  1. “genes”: GRanges对象，记录基因的坐标信息，起始位置和结束。必须要有一列是和”exons”对象中其中一列匹配
  2. “exons”: 记录每个基因外显子的坐标。必须要有一列和”genes”对象中的一列匹配
  3. “GRanges”: 记录TSS(转录起始位点)的坐标
1
2
3
4
5
geneAnnotation <- createGeneAnnotation(
  TSS = geneAnnotation$TSS,
  exons = geneAnnotation$exons,
  genes = geneAnnotation$genes
)

1.5.2 使用非标准基因组

ArchR会做一些必要的检查，来避免你做一些ArchR觉得”不符合常理”的操作。其中就是检查你的基因组注释的seqnames都需要以”chr”开头。大部分情况下这都没有问题，除了一些基因组的染色体并不都是以”chr”作为前缀（例如玉米）。如果用ArchR分析这些基因组，你需要告知ArchR忽略染色体名前缀，否则会报错停止。你需要在创建Arrow文件前，先运行addArchRChrPrefix(chrPrefix = FALSE) . 它会当前的R session里停止所有对染色体名前缀的检查操作。

此外，ArchR默认会将染色体名/seqnames转成字符串，因此如果你的seqnames都是数字，你需要以字符串形式提供这seqnames, 例如，你需要执行useSeqnames = c("1", "2", "3")，而不是useSeqnames = c(1, 2, 3)

你可以用getArchRChrPrefix随时检查当前R session是否需要染色体前缀。

1.6 创建Arrow文件

在本教程的后续部分，我们会使用Granja* et al. Nature Biotechnology 2019文章的数据进行展示，当然不是所有的数据集，我们会使用降抽样的造血细胞数据集，保证大部分人的电脑都能带动。该数据集包括了骨髓单核细胞(BMMC)和外周血单核细胞(PBMC)，以及CD34+造血干细胞和骨髓前体细胞(CD34 BMMC)。

我们下载的数据以fragment格式存放，记录每个比对序列在基因组上的位置。Fragments文件是10X Genomics分析平台的其中一个输出文件，或者你也可以从BAM文件进

一旦我们得到了fragment文件，我们将它们的路径记录在一个向量中，然后作为参数传给createArrowFiles(). 在构建过程中，一些基本的元信息和矩阵会增加到各个Arrow文件中，包括TileMatrix和GeneScoreMatrix. 其中TileMarix记录的以500-bp作为分窗统计染色体上各个位置上是否有insertion（具体见addTileMatrix）, GeneScoreMatrix则是基于邻近基因启动子的insetion数推断的基因表达量（见addGeneScoreMatrix()）。

教程用到的数据，可以用getTutorialData进行下载，大约为0.5G。

1
inputFiles <- getTutorialData("Hematopoiesis")

当然这一步实际是在本地建立一个HemeFragments目录，并下载指定数据，因此如果网络太差，可以自己尝试下载。

1
2
3
4
mkdir HemeFragments && cd HemeFragments
wget 'https://jeffgranja.s3.amazonaws.com/ArchR/TestData/HemeFragments/scATAC_BMMC_R1.fragments.tsv.gz'
wget 'https://jeffgranja.s3.amazonaws.com/ArchR/TestData/HemeFragments/scATAC_CD34_BMMC_R1.fragments.tsv.gz'
wget 'https://jeffgranja.s3.amazonaws.com/ArchR/TestData/HemeFragments/scATAC_PBMC_R1.fragments.tsv.gz'

在启动项目前，我们必须得设置ArchRGenome并设置线程数threads

1
2
addArchRGenome("hg19") # hg38, mm9, mm10
addArchRThreads(threads = 16)

从现在开始，我们将会用10-15分钟的时间创建Arrow文件。对每一个样本，都会有如下操作

  1. 从给定文件中读取开放信息(fragments)
  2. 为每个细胞计算质控信息(TSS富集得分和核小体信息)
  3. 根据质控参数过滤细胞
  4. 以500bp为窗口构建全基因组范围的TileMatrix
  5. 使用自定义的geneAnnotaiton创建GeneScoreMatrix, 其中geneAnnotation在我们调用addArchRGenome时定义
1
2
3
4
5
6
7
8
ArrowFiles <- createArrowFiles(
  inputFiles = inputFiles,
  sampleNames = names(inputFiles),
  filterTSS = 4, # 这个参数不需要过高，后续可以调整
  filterFrags = 1000,
  addTileMat = TRUE,
  addGeneScoreMat = TRUE
)

我们可以看下ArrowFiles对象，检查它是否真的是一个存放Arrow文件路径的向量

1
2
3
ArrowFiles
# [1] "scATAC_BMMC_R1.arrow"      "scATAC_CD34_BMMC_R1.arrow"
# [3] "scATAC_PBMC_R1.arrow"

1.7 细胞质控

scATAC-seq的严格质控对于剔除低质量细胞至关重要。在ArchR中，我们考虑数据的三种信息

  1. 每个细胞中唯一比对数(number of unique nuclear fragments)，不包括比对到线粒体的部分(unique nuclear fragments, 类似于单细胞转录组数据的表达的基因量)
  2. 信噪比(signal-to-background ratio)。如果是死细胞或者快死的细胞，那么DNA倾向于去染色质化，就会导致全局转座酶随机切割，体现出来就是信噪比低。
  3. fragment大小分布( fragment size distribution)。 由于核小体周期性，我们期望看到在147-bp附近出现一个低谷，因为缠绕一个核小体的DNA序列大约为147bp。

第一个参数, 唯一比对数非常的直观，如果一个细胞中的唯一比对太少，显然在后续分析中也没有太多可用价值，可以直接剔除掉。

第二个参数，信噪比是根据TSS富集分数进行计算。传统的混池ATAC-seq分析中，会使用TSS富集得分作为标准流程的一部分，用于确定信噪比（如 ENCODE计划）。我们和其他人通过混池ATAC-seq和scATAC-seq分析发现，TSS富集得分在大部分的细胞类型中都具有代表性。TSS富集得分的背后思想是，由于大蛋白复合体会结合在启动子区域，ATAC-seq数据更多的富集在基因的TSS区域而不基因组其他区域。通过检查这些TSS区域中心的开放水平，我们发现中心相对于两侧(两边的1900-2000 bp处)存在富集现象。因此，我们定义富集中心(TSS中心)相对于两侧区域的比值为TSS富集得分(TSS enrichment score)

传统上，我们会计算每个混池ATAC-seq样本中每个碱基的开放性，之后这个谱会被用于确定TSS富集得分。在scATAC-seq中通过该方法计算每个细胞的TSS富集得分速度较慢，并且需要很强的算力。为了提高计算效率，同时还能得到和传统计算接近的结果，我们以TSS位置为中心，以50-bp作为分窗计算两边的平均开放程度，之后该值除以TSS两侧位置(+-1900-200bp)的平均开放程度。 这种计算方法和原来相对比，两者的相关性大于0.99，并且结果几乎一样。

第三个参数fragment大小分布并不是特别重要，最好是人工检查下。由于DNA缠绕核小体的模式，我们预期在fragment大小分布中看到核小体的周期性分布。这些山峰和低谷的出现正是由于DNA缠绕0，1，2个核小体的结果(Tn5无法切割缠绕在核小体的DNA序列，只能切割两边）

ArchR默认会过滤TSS富集得分低于4或唯一比对数小于1000（也就是保留TSS富集得分大于4且唯一比对数大于1000的细胞）。切记，ArchR默认的参数最初是用于人类数据，不能直接用于其他物种。每个数据都有他的独特性，切勿生搬硬套，我们需要按照实际情况设置参数。一定要在createArrowFiles()运行前设置好该参数。

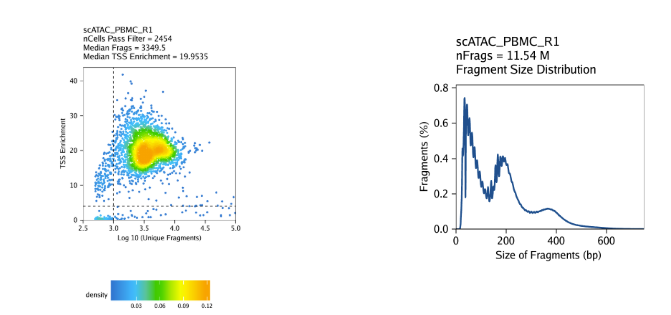
创建Arrow文件会在当前目录下生成一个”QualityControl”目录，这里面包括2个和样本相关的图。第一个图展示log10(unique nuclear fragments) vs TSS enrichment score, 虚线表示过滤阈值。第二图注释fragment大小分布图。

对我们的教程数据，我们的三个样本表现如下

BMMC:

BMMC

CD34+ BMMC:

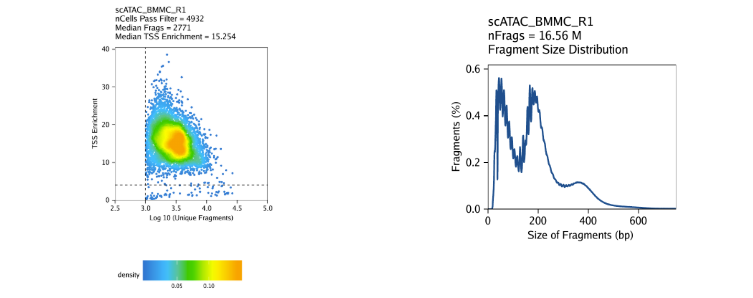
CD34 BMMC

PBMC:

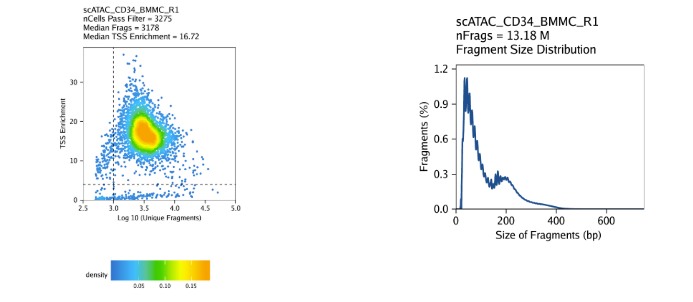
PBMC

我们现在整理完毕我们的Arrow文件，接下来就是创建ArchRProject了。

生信软件工具箱 | 基因组学

使用RaGOO将基因组提升至染色体水平

RaGOO

将染色体从contig/scaffold水平提升到chromosome水平是组装的最终目标。我们通常使用遗传图谱，光学图谱，HiC这些技术提供的信息将contig进行排序连接。

如果你组装的物种刚好有一个近源物种甚至说是同一物种，那其实我们可以直接将我们的contig比对到该基因组上，根据其提供的位置信息，将我们的contig/scaffold提高到染色体水平。RaGOO就是其中一款软件，相对于其他同类型的工具，它有以下优势

  • 不错的性能（感谢minimap2）
  • contig完整的排序和方向调整
  • GFF lift-over
  • 结构变异检测，整合了Assemblytics
  • 对于每个contig都计算可信得分

RaGOO使用minimap2将contig和reference进行比对，过滤低于1k的alignment，之后根据contig的覆盖度将contig聚类到最接近的染色体上，最后根据contig在染色体上的相对位置信息进行排序合并。

RaGOO基于Python3以及预先安装的minimap2。 我们需要从Github上克隆该项目进行安装

1
2
3
git clone https://github.com/malonge/RaGOO.git
cd RaGOO
python setup.py install

它的使用非常简单，就两个输入文件，contig和reference的FASTA文件

1
ragoo.py contigs.fasta reference.fasta

一些可供修改的参数:

  • e: 用于忽略reference一些序列
  • -gff: 将之前contig注释的GFF文件调整为当前版本
  • -b: 打断chimeric contig
  • -R: 提供额外的fastq/fasta序列辅助纠正错误组装
  • -T: 对应-R参数提供序列的类型， sr表示short read, corr表示纠错后的long reads
  • -t: 线程数
  • -g: 两个contig之间的gap大小
  • -s: 分析结构变异
  • -i: 最低得分用于将contig分组，默认是0.2
  • -j: 哪些contig序列需要忽略
  • -C: 将无法锚定的contig单独成行，而非合并成一个Chr0

几个建议: 默认线程是3，可以按照自己的需求进行提高。 如果对组装没有信心，可以加上-b -R -T参数用来纠正潜在的错误。我强烈推荐加上-C, 不然你会以为Chr0也是一个染色体。

可能的输出文件如下

1
2
3
4
5
6
ragoo_output/
├── ctg_alignments: 错误纠正结果
├── groupings     : 分组结果
├── orderings     : 排序结果
├── pm_alns       : 结构变异分析结果
└── ragoo.fasta   : 你需要的输出文件

在ragoo.fasta中，默认参数下Chr0_RaGOO表示contig.fasta的序列无法在reference.fa中定位，直接前后相连成一个序列。

个人主观评价： RaGOO使用容易，运行效率也很高，还能够分析结构变异。根据它的文章，有些时候表现还优于HiC组装结果，以后的一些基因组项目建议用上它。

HiC搞不定的情况

https://genomebiology.biomedcentral.com/articles/10.1186/s13059-019-1829-6

生信软件工具箱

使用Purge_dups去冗余序列

purge_dups能够根据read深度分析组装中haplotigs和overlaps。相对于另一款purge_haplotigs，它的运行速度更快，而且能够自动确定阈值。

purge_dups分为三个部分，第一部分是将序列回贴到基因组并分析覆盖度确定阈值，第二部分是将组装自我比对，第三部分是利用前两部分得到的信息鉴定到原来序列中的haplotigs和overlaps.

流程示意图

软件安装

尽管可以通过runner来进行程序调用，但是我更喜欢自己写脚本，因此不安装python3和runner

purge_dups是用C语言编写，因此需要通过make来编译

1
2
git clone https://github.com/dfguan/purge_dups.git
cd purge_dups/src && mak

脚本在scripts目录下，编译的程序在bin目录下

软件运行

输入文件分为两种，一种是组装序列，一种是测序数据。其中组装序列分为两种情况考虑，一种是类似falcon-unzip输出的primary assembly和alternative assembly，另一种则是单个组装文件。 而测序数据分为二代测序和三代ONT/PacBio测序。这里以单个组装文件输出和三代测序进行介绍，假定这两个输入文件分别命名为asm和reads.

第一步: 根据覆盖度计算分界点(cutoff)

1
2
3
4
5
# gzip可以替换成pigz, 进行多线程压缩
~/opt/biosoft/minimap2-2.17/minimap2 -t 80 -x map-pb $asm $reads | gzip -c - > pb_aln.paf.gz
# 统计paf, 输出PB.base.cov和PB.stat文件
~/opt/biosoft/purge_dups/bin/pbcstat pb_aln.paf.gz
~/opt/biosoft/purge_dups/bin/calcuts PB.stat > cutoffs 2> calcults.log

如果是二代测序，可以用bwa mem进行比对，然后用bin/ngscstat统计输出的bam文件覆盖度信息，然后用bin/calcuts计算分界点。

第二步: 将assembly从N处进行打断，如果assembly中没有N那就不会被打断，然后使用minimap2进行contig的自我比对。

1
2
3
4
# Split an assembly
~/opt/biosoft/purge_dups/bin/split_fa $asm > asm.split
# do a self-self alignment
~/opt/biosoft/minimap2-2.17/minimap2 -t 80 -xasm5 -DP asm.split asm.split | pigz -c > asm.split.self.paf.gz

这一步可以和前一步同时运行，两者互不影响。

第三步: 根据每个碱基的覆盖度以及组装的自我比对结果来对contig进行分类。

1
2
# purge haplotigs and overlap
~/opt/biosoft/purge_dups/bin/purge_dups -2 -T cutoffs -c PB.base.cov asm.split.self.paf.gz > dups.bed 2> purge_dups.log

dups.bed里的第四列就是每个contig的分类信息，分为”JUNK”, “HIGHCOV”, “HAPLOTIG”, “PRIMARY”, “REPEAT”, “OVLP” 这6类，其中只有

purge_dups可以先以默认参数进行运行，如果结果不理想，可以调整如下参数

  • -f默认是.8, 根据80%区域的覆盖度来对contig进行分类。例如80%的区域都低于5x，将该序列定义为JUNK。对应源码中的classify_seq函数的min_frac参数
  • -a和-b用来过滤alignment, 对于源码中的flt_by_bm_mm的min_bmf和min_mmf参数
  • -m表示将两个联配衔接时，最低的匹配碱基数
  • -M和-G:分别表示第一轮和第二轮将前后两个联配衔接时最大的空缺大小
  • -E表示 如果合并之后的alignment在contig末尾的前15k内，那么就把alignment延伸至contig末尾
  • -l: 用于控制overlap的大小，该值越小，overlap越多

第四步: 使用get_seqs根据dups.bed从原来的contig中提取主要组装和单倍型。

1
2
# get the purged primary and haplotigs sequences from draft assembly
~/opt/biosoft/purge_dups/bin/get_seqs dups.bed $asm

这里的purged.fa就是最终结果，junk, haplotig和duplication都会在hap.fa中。

可选步骤: 将alternative assembly和输出度hap.fa进行合并，然后运行上面四步，得到的purge.fa就是新的alternative assembly，而输出的hap.fa则是junk或overrepresented序列。

PS: 能不能用来过滤纯合基因组组装的垃圾序列呢？根据我对一个物种的测试，过滤前后的BUSCO值，几乎没有变化，missing rate只提高了0.1%，

1
2
3
4
# 运行前
C:98.8%[S:96.3%,D:2.5%],F:0.5%,M:0.7%,n:1375
# 运行后
C:98.7%[S:96.3%,D:2.4%],F:0.5%,M:0.8%,n:1375

因此我觉得这种用法是可行的，且Canu的作者也建议用purge_dups处理，参考canu-issues-1717。

另外，作者尚未在ONT和Illumina数据中测试该软件，但是作者认为只需要修改minimap2的-x map-pb为-x map-ont就可以用在ONT数据上。

转录组学

如何确定公共转录组数据集的来源性别

太长不看版: 文献报道XIST和RPS4Y1是区分性别的两个高可信度的标记基因，因此你没有必要去用其他性染色体上的基因去确定数据集的性别。

不仅仅是在使用公共的单细胞转录组数据，其实早在公共芯片数据或者RNA-seq数据挖掘中，就有人在考虑一个问题，这个数据的元信息作者会不会搞错了呢？

以性别为例，我们很容易想到表达Y染色体上基因数据肯定是男性，但是我们也知道基因也不是任何时刻都表达，所以如果一个Y染色体上的基因不表达，ta未必是女性。因此我们需要一个比较可靠的标记基因，来确保对性别的区别是正确的。

我最初的想法，也是对Y染色体的基因逐个看表达，但是转念想到，在我这个数据集中有用的标记未必适用于其他数据集呀。因此通过一波检索，我找到了一篇文献，里面给出了两个关键基因，XIST和RPS4Y1。

文献支持

接着我用Seurat提供的一个公共数据集进行测试，这个数据包括了不同技术处理的PBMC数据，预处理的代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
library(Seurat)
library(harmony)
data("pbmcsca")
library(dplyr)

pbmc <-  pbmcsca%>%
  Seurat::NormalizeData(verbose = FALSE) %>%
  FindVariableFeatures(selection.method = "vst", nfeatures = 2000) %>% 
  ScaleData(verbose = FALSE) %>% 
  RunPCA(pc.genes = pbmc@var.genes, npcs = 20, verbose = FALSE)

pbmc <- RunHarmony(pbmc, c("Experiment", "Method"))
pbmc <- RunUMAP(pbmc, reduction = "harmony", dims = 1:20)

最终我们获得了使用harmony去除批次效应后的数据集，接着我们用小提琴图分来源对XIST和RPS4Y1进行可视化

1
VlnPlot(pbmc, c("XIST","RPS4Y1"), group.by = "Method")

结果如下

小提琴图1

你会很奇怪为什么CEL-Seq2, Drop-Seq, InDrops, Seq-Well,Smart-seq2什么同时表达这两个基因呢？

很简单，因为这几种方法同时还包括两种实验，pbmc1和pbmc2

分群比较

当我们筛选所有的pbmc1实验进行展示

1
2
pbmc_sub <- subset(pbmc,  Experiment == "pbmc1")
VlnPlot(pbmc_sub, c("XIST","RPS4Y1"), group.by = "Method")

你会发现这两个是完美的互斥关系

pbmc1
如果你筛选出pbmc2进行展示

1
2
pbmc_sub <- subset(pbmc,  Experiment == "pbmc2")
VlnPlot(pbmc_sub, c("XIST","RPS4Y1"), group.by = "Method")

同样的，你得到一个完美的互斥结果

pbmc2

小结: XIST和RPS4Y1是区分性别的两个高可信度的标记基因，如果以后使用人的公共数据集的时候，可以用这个两个基因确定性别。

参考资料:

R

install.packages的参数介绍

今天解决解决了一个R包安装的问题，并且硬着头皮把install.packages和download.file的说明从头到位看了一遍，应该再也没有一个R包安装能为难到我了。

案例

问题描述

能够用浏览器访问镜像站点，但是在安装R包时遇到如下问题，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# CRAN
Warning in install.packages :
  unable to access index for repository https://mirrors.ustc.edu.cn/CRAN/src/contrib:
  cannot open URL 'https://mirrors.ustc.edu.cn/CRAN/src/contrib/PACKAGES'
Warning in install.packages :
  unable to access index for repository https://mirrors.ustc.edu.cn/CRAN/src/contrib:
  cannot open URL 'https://mirrors.ustc.edu.cn/CRAN/src/contrib/PACKAGES'
Warning in install.packages :
  package ‘ggtree’ is not available (for R version 3.5.1)
Warning in install.packages :
  unable to access index for repository https://mirrors.ustc.edu.cn/CRAN/bin/windows/contrib/3.5:
  cannot open URL 'https://mirrors.ustc.edu.cn/CRAN/bin/windows/contrib/3.5/PACKAGES'
# Bioconductor
Error: Bioconductor version cannot be validated; no internet connection?
In addition: Warning messages:
1: In library(package, lib.loc = lib.loc, character.only = TRUE, logical.return = TRUE,  :
  there is no package called ‘GSEABase’
2: In file(con, "r") : InternetOpenUrl failed: '??'
3: In file(con, "r") : InternetOpenUrl failed: 'on'

解决思路

第一步，确认R能否真的能够下载数据。检索到R用download.file进行文件下载，

1
2
download.file(url = "https://upload-images.jianshu.io/upload_images/2013053-6e5c996e3a0d4c93.png",
             destfile = "test.png")

发现无法直接下载内容，证明R在连接网络时出现了问题

1
2
3
4
5
6
trying URL 'https://upload-images.jianshu.io/upload_images/2013053-6e5c996e3a0d4c93.png'
Error in download.file(url = "https://upload-images.jianshu.io/upload_images/2013053-6e5c996e3a0d4c93.png",  : 
  cannot open URL 'https://upload-images.jianshu.io/upload_images/2013053-6e5c996e3a0d4c93.png'
In addition: Warning message:
In download.file(url = "https://upload-images.jianshu.io/upload_images/2013053-6e5c996e3a0d4c93.png",  :
  InternetOpenUrl failed:

第二步，根据报错信息, “InternetOpenUrl failed”进行检索，找到一种解决思路，也就是指定R访问网络的方法为libcurl

1
2
download.file(url = "https://upload-images.jianshu.io/upload_images/2013053-6e5c996e3a0d4c93.png",
              destfile = "test.png", methods="libcurl")

能够解决问题。

深入学习install.packages()

为了让自己能够更好解决R包安装问题，需要深入学习install.packages的原理(BiocManager::install本质上也是调用install.packages)。

先仔细阅读install.packages()的参数:

pkgs: 默认是包名，比如说”Matrix”, 会自动从CRAN上检索对应的包，然后进行下载。如果你希望指定安装本地包，或者一个具体的网络地址，参考代码如下:

1
2
3
4
# from url resource
install.packages("https://mirrors.tuna.tsinghua.edu.cn/CRAN/bin/windows/contrib/3.5/Matrix_1.2-15.zip", repos=NULL)
# from local
install.packages("~/../Desktop/Matrix_1.2-15.zip", repos = NULL)

  • lib: R包放在那里，和.libPaths()有关

  • repos: 镜像地址，当设置为NULL时，就可以安装本地包，或一个URLs。

  • contriburl: 这个参数不常用，一般是你自己搞了一个本地镜像点时使用，该参数会覆盖掉reops. 与type="both"不兼容

  • method: R包下载的方法，默认参数是default. 对于file://会调用internal，对于ftps://会调用libcurl,对于 http://,https://,ftp://, windows默认使用wininet,对于Unix类系统，默认使用libcurl. 注意：如果Windows上用capabilities("libcurl")返回时TRUE, 那么也可以用libcurl, Unix类系统无法使用wininet.

  • available: 可以是avaiable.packages返回的镜像点中可用R包，也可以设置为NULL(这时函数内部会自动调用avaiable.packages). 与type="both"不兼容

  • destdir: 下载的R包存放位置，NULL表示放在临时文件夹中，在关闭R后会被删除。

  • dependencies:默认是NA，表示 c("Depends", "Imports", "LinkingTo"), TRUE表示对于要安装的R包是c("Depends", "Imports", "LinkingTo", "Suggests")依赖，依赖的依赖是c("Depends", "Imports", "LinkingTo", "Suggests"). 注意： 对于二进制包，都会忽略”LinkingTo”

  • type: 下载的是二进制包(“binary”)还是源代码”source”. 如果设置为”binary”, 依旧会先去检查该软件包最新的版本是否只有源代码，可用options(install.packages.check.source = "no")关闭。当设置为”source”时，只有不含”C/C++/Fortran”代码的R包可以被编译，如果R包中有C/C++/Fortran代码，那么Windows就需要安装Rtools。注意： 在Windows编译R包时，有一小部分需要设置INSTALL_opts = "--force-biarch" 或INSTALL_opts = "--merge-multiarch", 建议后者。

  • configure.args: 该参数只在源代码编译时使用，会传入R CMD INSTALL中

  • configure.vars: 该参数只在源代码编译时使用， 类似于configure.args, 效果是在运行configure前设置环境变量。

  • clean: 在R CMD INSTALL中加入--clean参数，用于清除临时中间文件。

  • Ncpus： 编译时用多少CPU，加快编译速度。

  • verbose: 是否输出安装时的信息。

  • libs_only: 是否只安装64位或者32位的动态链接库

  • INSTALL_opts: 源代码编译时R CMD INSTALL的额外传入参数，例如c("--html", "--no-multiarch", "--no-test-load").

  • quiet: 安静模式，降低输出的信息量

  • keep_outputs: 是否在当前工作目录下保留源代码编译后的输出文件。

  • ...的额外的参数来自于download.file, 主要就是cache=TRUE表示服务端缓存。默认是”TRUE”，如果是http://和https://更建议用cacheOK=FALSE`, 避免一些报错。

关于Secure URLs

对于https://或者ftps://这类URL，R在下载数据时会尝试对网站的证书进行验证。通常会调用操作系统安装的CA root certificates完成。

对于Windows系统，method="libcurl"时可能会出现问题，也就是Windows系统不提供有效的CA certificate bundle, 也就是说默认情况下，Windows的certificates是没有被验证过的。也就是Sys.getenv("CURL_CA_BUNDLE")返回结果为空，建议Sys.setenv(CURL_CA_BUNDLE=file.path(Sys.getenv("R_HOME"),"/etc/curl-ca-bundle.crt"))打开验证。

可以从https://raw.githubusercontent.com/bagder/ca-bundle/master/ca-bundle.crt下载curl-ca-bundle.crt的备份。

关于代理

wininet调用系统中的Internet Option处理代理(proxy). 或者用Sys.setenv设置环境变量http_proxy,ftp_proxy

互联网选项Internet Options

解决报错的一些建议

建议1：在用install.packages安装R包之前，先用update.packages()升级一下已有R包。

建议2：对于文章开头的报错，请修改~/.Rprofile，增加如下内容

1
2
3
4
5
options("download.file.method"="libcurl")
# # getOption("download.file.method")
options("url.method"="libcurl")
# getOption("url.method")
# options(internet.info = 0) # 进行HTTP传输的诊断，默认是2，只会显示最后的出错信息

也就是Windows尽量设置默认的method为libcurl，因为wininet未必一直支持HTTPS。 –https://github.com/r-lib/remotes/issues/45#issuecomment-262955721

建议3：如果遇到编译源代码报错，请在install.packages()中设置参数INSTALL_opts = "--merge-multiarch"和clean=TRUE

建议4：如果有些R包在安装时不能正确处理依赖关系，请在install.packages()中设置参数depencies=TRUE

生信软件工具箱

Apollo安装笔记

当我们通过一些流程化工具对一个基因组进行注释之后，最终得到的注释结果(通常是GFF文件)或多或少存在一些注释错误，需要通过人工校正。

我们的目标是安装一个能够在自己服务器使用的Apollo用于人工注释，以下的操作都需要用到管理员权限。

Docker

既然都得用到管理员权限，我们优先使用Docker的方法进行安装。

第一步: 获取Docker镜像

1
docker pull gmod/apollo

第二步: 启动

1
docker run -d -it --privileged --rm -p 9999:8080 -v /tmp/apollo_data gmod/apollo

最后就可以打开网页，输入服务器IP:9999即可打开网页

默认的账号admin@local.host，密码是password

登录

常规方法

第一步: 安装必须的依赖环境

1
sudo yum install zlib zlib-dev expat-dev libpng-dev libgd2-noxpm-dev build-essential git python-software-properties python make

第二步: 安装Java开发环境，至少是Java8

1
yum install java-1.8.0-openjdk

第三步: 安装Tomcat用于部署服务

1
yum install tomcat

使用vim，在/usr/share/tomcat/conf/tomcat.conf最后一行加入如下内容，提高运行内存

1
JAVA_OPTS="-Xms512m -Xmx2g -XX:+CMSClassUnloadingEnabled -XX:+CMSPermGenSweepingEnabled -XX:+UseConcMarkSweepGC"

假如基因组有超过1000的scaffolds，且有40个人同时处理一个项目，可以用如下的参数

1
2
3
4
5
6
7
8
JAVA_OPTS="-Xmx12288m -Xms8192m \
        -XX:ReservedCodeCacheSize=64m \
        -XX:+UseG1GC \
        -XX:+CMSClassUnloadingEnabled \
        -Xloggc:$CATALINA_HOME/logs/gc.log \
        -XX:+PrintHeapAtGC \
        -XX:+PrintGCDetails \
        -XX:+PrintGCTimeStamps"

使用vim编辑/usr/share/tomcat/conf/server.xml, 找到Connector port所在行，将其中的8080修改成合适的端口号

1
2
3
<Connector port="8080" protocol="HTTP/1.1"
               connectionTimeout="20000"
               redirectPort="8443" />

启动和停止Tomcat服务

1
2
tomcat start
tomcat stop

第四步: 安装nodejs和yarn。nodejs的版本在6-12之间都是可行的，我们可以使用nvm管理nodejs。

1
2
3
curl -o- https://raw.githubusercontent.com/nvm-sh/nvm/v0.35.3/install.sh | bash
nvm install 8
npm install -g yarn

第五步: 下载并解压缩Apollo

1
2
3
wget https://github.com/GMOD/Apollo/archive/2.5.0.zip
unzip 2.5.0.zip
cd Apollo-2.5.0

第六步: 配置数据库。Apollo支持H2, Postgres, MySQL，对应三个不同的配置文件

  • sample-h2-apollo-config.groovy
  • sample-postgres-apollo-config.groovy
  • sample-mysql-apollo-config.groovy

可以按照需要将对应的文件重命名为apollo-config.groovy。默认情况下使用H2作为数据库。

如果需要用MySQL，需要先为apollo建立账号并授权

1
2
3
4
5
6
7
8
9
10
11
12
# Login to mysql e.g., 
mysql -u root -p
# Create a user 
CREATE USER 'apollo'@'localhost' IDENTIFIED BY 'THE_PASSWORD';
# Create Database
CREATE DATABASE `apollo`;
CREATE DATABASE `apollo-test`;
CREATE DATABASE `apollo-production`;
# grant
GRANT ALL PRIVILEGES ON `apollo`.* To 'apollo'@'localhost';
GRANT ALL PRIVILEGES ON `apollo-test`.* To 'apollo'@'localhost';
GRANT ALL PRIVILEGES ON `apollo-production`.* To 'apollo'@'localhost';

接着复制模板

1
cp sample-mysql-apollo-config.groovy apollo-config.groovy

然后更改apollo-config.groovy 中的username和password，也就是apollo和THE_PASSWORD。

个人建议: 有限选择H2数据库。

第七步: 使用vim修改配置文件grails-app/conf/Config.groovy

common_data_directory: 用户上传数据的目录，需要设置一个所有人都有权限访问的目录，例如

1
common_data_directory = "/opt/temporary/apollo_data"

然后建立对应的文件夹并更改权限

1
2
3
mkdir -p /opt/temporary/apollo_data
chown tomcat /opt/temporary/apollo_data
chgrp tomcat /opt/temporary/apollo_data

第八步: 部署apollo。

虽然只需要运行./apollo deploy即可，但是由于网络原因，可能会出现如下的报错

1
ERROR: Failed to download Chromium r672088! Set "PUPPETEER_SKIP_CHROMIUM_DOWNLOAD" env variable to skip download.

因此，需要先运行如下代码，修改镜像

1
npm config set puppeteer_download_host=https://npm.taobao.org/mirrors

最终会在target目录下生成一个以war结尾的文件，例如apollo-2.5.0.war, 该文件需要用Tomcat进行部署。

1
cp target/apollo-2.5.0.war /usr/share/tomcat/webapps/apollo.war

复制之后需要等待一段时间，才能打开对应的网页服务器IP:端口/apollo，第一次登陆需要先注册账号（随意填写）。

登录界面

如果你发现出现了如下的警告，把其中的apollo_data改成/tmp即可

无写入权限

软件逻辑

软件分为用户端和服务器端。网页端基于Jbrowse，增加了Annotation Track，用于编辑新的注释信息，以及一个管理数据的侧边栏。

而服务端则分为三个部分，中间部分是基于Java开发的Apollo服务，用于和数据库端、文件系统交互。数据库端存放

Apollo服务端使用了Grails，一套用于快速Web应用开发的开源框架，它基于Groovy编程语言，并构建于Spring、Hibernate等开源框架之上，是一个高生产力一站式框架。数据库端目前主力是关系型数据库，例如PostgreSQL、MySQL和H2，将来还有Chado这种图数据库。文件系统端则是用户提供的各种生物学数据。

软件逻辑

Citing Apollo: Dunn, N. A. et al. Apollo: Democratizing genome annotation. PLoS Comput. Biol. 15, e1006790 (2019)

数据结构与算法

深入解读Khash.h

C语言标准库并没有字典(map)和集合(set)这种数据结构，因此如果想需要在C语言使用这种数据结构，要么自己根据不同数据类型都写一种函数，或者就是用别人写好的数据结构来用。

Khash.h提供了一种基于开放寻址法的泛型的哈希表, 这里的开放寻址法是一种解决哈希冲突的方法，当哈希函数时计算的位置已经有元素的时候，它会基于当前位置往后探测(probe), 找到一处没有元素的位置。当然还有一种方法，就是拉链法，也就是在冲突的地方，创建一个链表，里面存放具有相同哈希地址的不同元素。

哈希函数

khash.h根据不同的初始化函数会替换成不同的哈希函数，一共有是那种int,int64和str

1
2
3
#define kh_int_hash_func(key) (khint32_t)(key)
#define kh_int64_hash_func(key) (khint32_t)((key)>>33^(key)^(key)<<11)
#define kh_str_hash_func(key) __ac_X31_hash_string(key)

int就是将原值转换成khint32_t，int64用到了位运算，通过右移，按位异或和左移操作，最后转换成khint32_t。这两个哈希函数都非常简单，降低了哈希函数计算的时间。

稍微复杂的就是字符串的哈希函数， 它的计算方式如下

1
2
3
4
5
6
static kh_inline khint_t __ac_X31_hash_string(const char *s)
{
	khint_t h = (khint_t)*s;
	if (h) for (++s ; *s; ++s) h = (h << 5) - h + (khint_t)*s;
	return h;
}

此外还有一个在2011-09-16 (0.2.6)增加的哈希函数kh_int_hash_func2, 能够比较好的处理一些不怎么随机的数据，它的计算过程就非常的复杂了，默认不启用,。

1
2
3
4
5
6
7
8
9
10
11
12
13

static kh_inline khint_t __ac_Wang_hash(khint_t key)
{
    key += ~(key << 15);
    key ^=  (key >> 10);
    key +=  (key << 3);
    key ^=  (key >> 6);
    key += ~(key << 11);
    key ^=  (key >> 16);
    return key;
}
#define kh_int_hash_func2(key) __ac_Wang_hash((khint_t)key)

数据结构

数据结构通常和算法都是搭配使用，因此理解这个数据结构的设计，就能理解后续的代码逻辑。

khash.h的定义的kh_##name##_t数据结构一共有7个部分

  • n_buckets: 记录桶的数目，也就是哈希表的空间
  • size: 当前记录元素
  • n_occupied: 当前占据的多少元素
  • upper_bound: 上限大小
  • flags: 记录当前位置是否有数据
  • keys: 指向key的指针
  • vals: 指向value的指针
1
2
3
4
5
6
7
#define __KHASH_TYPE(name, khkey_t, khval_t) \
	typedef struct kh_##name##_s { \
		khint_t n_buckets, size, n_occupied, upper_bound; \
		khint32_t *flags; \
		khkey_t *keys; \
		khval_t *vals; \
	} kh_##name##_t;

关于桶的大小n_buckets:作者以2的n次方大小，保证有足够的空间，降低哈希碰撞。

关于size和n_occupied: 之所以有两个变量来记录哈希表中的元素，是为了降低删除运算。我们不需要在每一次删除运算时，都进行内存的释放和调整，而只要将对应的位置标记为删除状态即可，也就是减少size，而不减少n_occupied.

关于上限upper_bound: 当桶剩下的空间不够时，那么出现哈希碰撞的概率就会变大，因此就需要对哈希表进行调整，计算公式如下。

1
2
tatic const double __ac_HASH_UPPER = 0.77;
h->upper_bound = (khint_t)(h->n_buckets * __ac_HASH_UPPER + 0.5);

剩下的flags,keys和vals都是指针，用于指向实际地址，是实际记录数据类型的数据结构。

1
2
3
4
new_flags = (khint32_t*)kmalloc(__ac_fsize(new_n_buckets) * sizeof(khint32_t));
memset(new_flags, 0xaa, __ac_fsize(new_n_buckets) * sizeof(khint32_t)); 
khkey_t *new_keys = (khkey_t*)krealloc((void *)h->keys, new_n_buckets * sizeof(khkey_t)); 
khval_t *new_vals = (khval_t*)krealloc((void *)h->vals, new_n_buckets * sizeof(khval_t));

示意图

具体的赋值和删除操作，在后续介绍。

初始化、清空和删除

khash使用kcalloc(等同于calloc)申请一个大小为1的kh_##name##_t, 所有元素默认值都是0.

1
2
3
SCOPE kh_##name##_t *kh_init_##name(void) {							\
    return (kh_##name##_t*)kcalloc(1, sizeof(kh_##name##_t));		\
                                          }

SCOPE第一层替换代码是static kh_inline klib_unused, 第二层替换就是static inline __attribute__ ((__unused__)). static inline用于提高函数的执行效率，但是此类函数如果没有被使用，编译器会有警告，但是定义了__attribute__ ((__unused__))就可以避免这种警告。

因此，SCOPE是一种提高代码执行效率的函数修饰符。

和初始化相对的操作，一种是清空表里的元素，也就是将size和n_occupied都设置为0，把所有的flags都设置为0xaa也就是为空

1
2
3
4
5
6
7
SCOPE void kh_clear_##name(kh_##name##_t *h)						\
	{																	\
		if (h && h->flags) {											\
			memset(h->flags, 0xaa, __ac_fsize(h->n_buckets) * sizeof(khint32_t)); \
			h->size = h->n_occupied = 0;								\
		}																\
	}

另一种是直接释放所有内存。但它不会释放你在堆(heap)中申请的动态内存），也就是你需要自己手动释放你为字符串类型的key和value申请的内存。

1
2
3
4
5
6
7
8
SCOPE void kh_destroy_##name(kh_##name##_t *h)						\
	{																	\
		if (h) {														\
			kfree((void *)h->keys); kfree(h->flags);					\
			kfree((void *)h->vals);										\
			kfree(h);													\
		}																\
	}																	\

状态(flag)设置和查询

在kh_##name##_t数据结构中，flags用于记录不同位置的状态。为了节约空间，flags用的1/16的桶大小来记录信息。

这是因为flags是一个指向khint32_t元素的指针，khint32_t表示的是32位无符号整型，如果使用2个二进制位表示状态，那么一个32位无符号整型就能记录16个元素。

1
2
3
#define __ac_fsize(m) ((m) < 16? 1 : (m)>>4)
new_flags = (khint32_t*)kmalloc(__ac_fsize(new_n_buckets) * sizeof(khint32_t));
memset(new_flags, 0xaa, __ac_fsize(new_n_buckets) * sizeof(khint32_t));

那么这里有一个问题，为啥不用一个二进制位来表示每个位置的状态呢？这是因为记录的状态有4种，分别是

  • empty(10): 空，没有存放key

  • delete(01), 虽然有key，但是标记为删除

  • either(11): 要么是空，要么是删除了，总之可以放key

  • occupied(00): 已经占用了元素

所以，必须要用2个二进制位。使用memset设置的0xaa对应二进制的0b10101010， 表示默认状态是empty.

下面这四行用于设置第i位的状态

1
2
3
4
#define __ac_set_isdel_false(flag, i) (flag[i>>4]&=~(1ul<<((i&0xfU)<<1)))
#define __ac_set_isempty_false(flag, i) (flag[i>>4]&=~(2ul<<((i&0xfU)<<1)))
#define __ac_set_isboth_false(flag, i) (flag[i>>4]&=~(3ul<<((i&0xfU)<<1)))
#define __ac_set_isdel_true(flag, i) (flag[i>>4]|=1ul<<((i&0xfU)<<1))

在设置第i位状态时，也就是设置i右移四位(也就是除以16)的状态，接着用((i&0xfU)<<1))计算出状态左移步数，例如i=17时，左移2位，i=16时, 左移0位。

如果我们设置的是is(del|empty|both)_false, 也就是需要反向设置，那么还需要对状态按位取反。接着和原来的情况按位与操作。

相对于设置状态，提取状态就变得容易些，只需要提取对应位置的状态，然后左移，然后和状态进行按位与运算即可。

1
2
3
#define __ac_isempty(flag, i) ((flag[i>>4]>>((i&0xfU)<<1))&2)
#define __ac_isdel(flag, i) ((flag[i>>4]>>((i&0xfU)<<1))&1)
#define __ac_iseither(flag, i) ((flag[i>>4]>>((i&0xfU)<<1))&3)
  • ul: unsigned long, 无符号长整型
  • 0xfU: f就是10进制的16, U表示unsigned(无符号)，等价于2进制的0b1111U

如果是我设计flag的话，我估计会申请一个和key大小一样内容空间，直接用1/2/3的数字来表示，而不会用到位运算了。

key、value相关操作

当我们的键值对中的key=1001, 我们是不可能申请一个1001大小的数组用于存放key。否则，当我们要存放key=1和key=10001,我们就会浪费大量的内存空间。为了根据key查询对应的value，我们也需要申请同样大小的空间，那么就会浪费大量的空间。

为了节约空间，我们只会有和桶等大小的内存空间，来放key和value

1
2
khkey_t *new_keys = (khkey_t*)krealloc((void *)h->keys, new_n_buckets * sizeof(khkey_t));
khval_t *new_vals = (khval_t*)krealloc((void *)h->vals, new_n_buckets * sizeof(khval_t));

那么面对一个范围比较大的key，我们如何将key映射到有限大小的桶中呢？ 在讲解实际代码之前，我们先以几个具体的例子讲解背后的逻辑。

假如目前的桶大小为16(n_buckets=16), 但是我们的key是10001，我们是无法直接将key放入桶中。由于32位整型的哈希函数就是返回原值，那么 k=10001，显然依旧无法放入桶中。这个时候，我们就需要引入一个取模的概念，所谓的取模，就是将我们的key和桶的大小相除，得到剩下的余数，也就是 10001 % 16 = 1，也就是在index=1的位置存放key。取模保证了我们再大的数字都能落在一个固定范围内，例如 1223423423423 % 16 = 15。为了提高取模运算，我们可以用一个等价的位运算10001 & 15来加速，15的二进制表示为0b01111，也就是无论一个数字有多大，最终只有最后的四位可以不为0.

取模操作会有一个问题，就是不同的数字会有相同的余数，例如17求余之后也是1。那么此时应该处理呢？解决方法有很多种，khash.h采用的方法就是，在冲突的地方往后找空位。也就是，我们可以在2的位置插入17。

在查询操作的时候，也不能直接返回模运算得到的位置，而是将位置的key和我们查询的key进行比较，如果相同才能返回。

除了插入和查询外，我们还有一个删除操作。为了提高效率，我们执行删除操作时，需要将对应位置标记为删除态即可，等到空间存在过多的删除位置时，我们才考虑做一次空间调整。

khash.h中kh_put_##name,kh_get_##name这两个函数都需要根据key计算index分别对应

  • 根据给定的key获取桶的位置，并在keys对应的位置上加入计算后的key
  • 根据给定的key查询桶的位置

有了桶具体位置之后，kh_key,kh_val,kh_del_##name就可以对key和value进行修改或删除。

接下来的部分就是具体的代码讲解

put

kh_put_##name,对应khash.h的307-348行，分两个部分

第一部分，判断当前占用元素(n_occupied)是否超出了可容纳元素的上限(upper_bound) ，也分为两种情况，一种是真的满了，另一种是大部分都是删除状态）, 如果是的话，就需要调整哈希表的大小（在下一部分介绍），如果调整失败，会直接返回当前桶的最后一个位置。否则会进入第二部分

1
2
3
4
5
6
7
8
9
if (h->n_occupied >= h->upper_bound) { /* update the hash table */ \
	if (h->n_buckets > (h->size<<1)) {							\
		if (kh_resize_##name(h, h->n_buckets - 1) < 0) { /* clear "deleted" elements */ \
				*ret = -1; return h->n_buckets;						\
		}														\
	} else if (kh_resize_##name(h, h->n_buckets + 1) < 0) { /* expand the hash table */ \
				*ret = -1; return h->n_buckets;							\
	}
} /* TODO: to implement automatically shrinking; resize() already support shrinking */ \

注意，这里的ret, 一共有-1, 0, 1, 2 这四种状态，分别表示操作失败，key在表中出现，桶为空，桶是删除状态

第二部分，根据key计算index，找到待插入桶的位置，代码一共有7个变量

1
2
3
khint_t x;
khint_t k, i, site, last, mask = h->n_buckets - 1, step = 0; \
x = site = h->n_buckets; k = __hash_func(key); i = k & mask; \
  • x: 最终返回的位置
  • k: 根据key计算哈希值
  • i: 哈希值基于mask的求模结果
  • site: 上一个标记删除的位置
  • last: 第一次算出的i的位置
  • mask: 用于对i进行求模
  • step: 哈希冲突后的往后移动的步数

查找可用位置的代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
if (__ac_isempty(h->flags, i)) x = i; /* for speed up */	\
else {\
	last = i; \
	while (!__ac_isempty(h->flags, i) && (__ac_isdel(h->flags, i) || !__hash_equal(h->keys[i], key))) {\
		if (__ac_isdel(h->flags, i)) site = i;				\
			i = (i + (++step)) & mask; \
			if (i == last) { x = site; break; }					\
	}														\
	if (x == h->n_buckets) {\
		if (__ac_isempty(h->flags, i) && site != h->n_buckets) x = site; \
		else x = i;											\
	}														\
}															\

即便最简单的情况是__ac_isempty(h->flags, i),也就是待插入的位置为空，也要分为三种情况考虑，

  • 没有碰撞: x = i, site=h->n_buckets
  • 出现碰撞，往后探测过程中没有删除位置: x=site=h->n_buckets
  • 出现碰撞，往后探测过程中有删除位置: x=h->buckets, site=i

如果不为空，那么考虑key重复的情况，也就是待插入的位置的哈希值和当前key的哈希值相同，也就是!__ac_isdel(h->flags, i) && __hash_equal(h->keys[i], key)), 也分为两种请

  • 没有碰撞，x=site=h->n_buckets
  • 出现碰撞，往后探测过程中没有删除位置: x=site=h->n_buckets
  • 出现碰撞，往后探测过程中有删除位置: x=h->buckets, site=i

最麻烦的情况是，找了一圈，回到最初的位置i=last, 那么此时x=site=i

不存在所有元素都是delete，或者所有元素都是occupied的情况，因为一旦超过一个容纳上线，哈希表会自动扩容。

最后，如果x!=h->n_buckets, 我们是找了一圈，我们直接使用上一个标记为删除的位置，否则考虑两种情况

  1. 如果找到的位置为空，且中间有删除的位点的话，我们优先用删除的位置
  2. 换言之，找到的位置不为空，或者中间没有删除位置，那就用有相同哈希的位置或者中间的空位
1
2
3
4
if (x == h->n_buckets) {								\
	if (__ac_isempty(h->flags, i) && site != h->n_buckets) x = site; \ 
	else x = i;											\
}														\

最后，分三种情况考虑

  • 如果是x的位置为空，标记状态，并增加size和n_occupied
  • 如果是x的位置标记为删除，标记状态，只增加size
  • 否则就说明是重复元素，不做任何操作，返回状态是0
1
2
3
4
5
6
7
8
9
10
11
if (__ac_isempty(h->flags, x)) { /* not present at all */		\
	h->keys[x] = key;											\
	__ac_set_isboth_false(h->flags, x);							\
	++h->size; ++h->n_occupied;									\
	*ret = 1;													\
} else if (__ac_isdel(h->flags, x)) { /* deleted */				\
	h->keys[x] = key;											\
	__ac_set_isboth_false(h->flags, x);							\
	++h->size;													\
	*ret = 2;													\
} else *ret = 0; /* Don't touch h->keys[x] if present and not deleted */ \

get

kh_get_##name的含义是 查询，根据给定的key，在哈希表中查找是否有元素，并返回哈希表对应的位置。由于存在哈希冲突的可能，因此查询过程中还需要比较查询的key和哈希表记录的key值是否相同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
SCOPE khint_t kh_get_##name(const kh_##name##_t * h, khkey_t key) 	\
	{																	\
		if (h->n_buckets) {												\
			khint_t k, i, last, mask, step = 0; \
			mask = h->n_buckets - 1;									\
			k = __hash_func(key); i = k & mask;							\
			last = i; \
			while (!__ac_isempty(h->flags, i) && (__ac_isdel(h->flags, i) || !__hash_equal(h->keys[i], key))) { \
				i = (i + (++step)) & mask; \
				if (i == last) return h->n_buckets;						\
			}															\
			return __ac_iseither(h->flags, i)? h->n_buckets : i;		\
		} else return 0;												\
	}

一共定义了5个变量

  • k: k是哈希函数计算结果
  • i: 存放key和value值的索引(index)
  • last: 起始的index
  • mask: 用于取模，将key限制在桶大小以内
  • step: 哈希碰撞后，往后移动

如果理解了插入的逻辑，那么查询的逻辑其实更简单。查询的目标是找到被占用的位置，且该位置上的key的哈希值和我们查询的key的哈希值相同。

delete

kh_del_##name操作最为简单，就是根据你提供的index（注意他是需要你提供key计算好的index），来标记桶对应位置为删除状态，但不会实际释放对应位置上key和value的内容。删除的时候，我们得保证索引位置不是桶的最后一个位置，也不是空状态或者删除状态。

1
2
3
4
5
6
7
SCOPE void kh_del_##name(kh_##name##_t * h, khint_t x)				\
	{																	\
		if (x != h->n_buckets && !__ac_iseither(h->flags, x)) {			\
			__ac_set_isdel_true(h->flags, x);							\
			--h->size;													\
		}																\
	}

调整空间

显然初始化内存大小是无法记录元素的，以及如果新增元素超过当前哈希表所能容纳的大小，或者哈希表中大部分的元素都被删除，不需要那么多空间，我们都需要对哈希表的空间进行调整。因此在khash.h有62行代码，即244-306，是负责哈希表的大小调整。

khash.h代码中只有kh_put_##name在h->n_occupied >= h->upper_bound时会调用kh_resize_##name，而且是先考虑h->n_buckets > (h->size<<1), 如果桶大小比实际存放元素数的2倍还大，说明是标记删除元素太多了，那么需要清空哈希表，否则是真的不够了。前者传给kh_resize_##name的new_n_buckets = h->n_buckets - 1, 后者new_n_buckets = h->n_buckets + 1

n_buckets会先经过kroundup32函数计算出新哈希表的大小（new_n_buckets），kroundup32涉及到一系列的位运算

1
#define kroundup32(x) (--(x), (x)|=(x)>>1, (x)|=(x)>>2, (x)|=(x)>>4, (x)|=(x)>>8, (x)|=(x)>>16, ++(x))

它的效果是得到比当前桶的大小大且距离最近的2^n,例如桶的数目是55，那么最近的就是64。如果桶的数目是297, 那么最近的就是512，如果是64，那么就是63。 如果是我写那就只能写出下面这种代码 

1
2
3
4
5
6
7
8
9
int roundup32(int x) {
	int tmp = x;
	int y = 1;
	while (tmp) {
		tmp >>= 1;
		y <<= 1;
	}
	return x==(y>>1) ? y>>1 : y;
}

接着，它还保证桶的数目最少是4，if (new_n_buckets < 4) new_n_buckets = 4;

我们先考虑申请的空间的可容纳上限比已有元素多的情况

1
if (h->size >= (khint_t)(new_n_buckets * __ac_HASH_UPPER + 0.5)) j = 0;

khash.h会先计算new_flags的数目，并初始化为0xaa. 如果当前的桶的大小低于新的桶的大小，那么就用krealloc重新申请内存，并将数据拷贝到新的内存地址中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
new_flags = (khint32_t*)kmalloc(__ac_fsize(new_n_buckets) * sizeof(khint32_t));	\
if (!new_flags) return -1;								\
memset(new_flags, 0xaa, __ac_fsize(new_n_buckets) * sizeof(khint32_t)); \
if (h->n_buckets < new_n_buckets) {	/* expand */		\
	khkey_t* new_keys = (khkey_t*)krealloc((void*)h->keys, new_n_buckets * sizeof(khkey_t)); \
	if (!new_keys) { kfree(new_flags); return -1; }		\
		h->keys = new_keys;									\
		if (kh_is_map) {
			\
				khval_t* new_vals = (khval_t*)krealloc((void*)h->vals, new_n_buckets * sizeof(khval_t)); \
				if (!new_vals) { kfree(new_flags); return -1; }	\
					h->vals = new_vals;								\
		}													\
} /* otherwise shrink */

上面的代码相对简单，最复杂的268-294行重新计算hash的过程。重新计算哈希的本质本质就是缩小哈希表。

因为桶的大小是按照4,8,16,32,64,128,256,512,1024这种方式增加，所以只要是增加空间，当前的元素数目是不可能高于新的桶大小的可容纳范围的上限的。只有在h->n_buckets <= (h->size<<1)的情况下，也就是当前空间一般都是删除的元素的情况下，才会出现当前元素数目大于桶的可容纳上限的情况。

此时新的空间大小变为原来的一半，那么里面的元素就需要移动位置。搬运的时候，很有可能出现哈希碰撞。

搬运过程是一个嵌套循环，外层循环遍历旧哈希表的每个桶，如果发现它该位置上有元素，就记录它的key和value，然后我们算下它在新哈希表位置（如果找到不为空的，就往后移动），并将新位置标记为不为空。同时检查新哈希表位置对应的旧哈希表位置上是否有元素，如果有，就把该元素和待插入元素进行交换，我们的下一个任务就是为这个元素查找位置，否则就可以退出了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
for (j = 0; j != h->n_buckets; ++j) {
	\
		if (__ac_iseither(h->flags, j) == 0) {
			\
				khkey_t key = h->keys[j];							\
				khval_t val;										\
				khint_t new_mask;									\
				new_mask = new_n_buckets - 1; 						\
				if (kh_is_map) val = h->vals[j];					\
					__ac_set_isdel_true(h->flags, j);					\
					while (1) { /* kick-out process; sort of like in Cuckoo hashing */ \
						khint_t k, i, step = 0; \
						k = __hash_func(key);							\
						i = k & new_mask;								\
						while (!__ac_isempty(new_flags, i)) i = (i + (++step)) & new_mask; \
							__ac_set_isempty_false(new_flags, i);			\
							if (i < h->n_buckets && __ac_iseither(h->flags, i) == 0) { /* kick out the existing element */ \
							{ khkey_t tmp = h->keys[i]; h->keys[i] = key; key = tmp; } \
								if (kh_is_map) { khval_t tmp = h->vals[i]; h->vals[i] = val; val = tmp; } \
									__ac_set_isdel_true(h->flags, i); /* mark it as deleted in the old hash table */ \
							}
							else { /* write the element and jump out of the loop */ \
								h->keys[i] = key;							\
								if (kh_is_map) h->vals[i] = val;			\
									break;										\
							}												\
					}													\
		}														\
}

接下来的工作就是用krealloc重新调整内存大小, 重新计算其他元信息.

1
2
3
4
5
6
7
8
9
if (h->n_buckets > new_n_buckets) { /* shrink the hash table */ \
h->keys = (khkey_t*)krealloc((void*)h->keys, new_n_buckets * sizeof(khkey_t)); \
if (kh_is_map) h->vals = (khval_t*)krealloc((void*)h->vals, new_n_buckets * sizeof(khval_t)); \
}															\
kfree(h->flags); /* free the working space */				\
h->flags = new_flags;										\
h->n_buckets = new_n_buckets;								\
h->n_occupied = h->size;									\
h->upper_bound = (khint_t)(h->n_buckets * __ac_HASH_UPPER + 0.5); \
数据结构与算法

一次由爬楼梯和零钱兑换II引起的DP子问题定义思考

在LeetCode上有两道题目非常类似，分别是

如果我们把每次可走步数/零钱面额限制为[1,2], 把楼梯高度/总金额限制为3. 那么这两道题目就可以抽象成”给定[1,2], 求组合成3的组合数和排列数”。

接下来引出本文的核心两段代码，虽然是Cpp写的，但是都是最基本的语法，对于可能看不懂的地方，我加了注释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution1 {
public:
    int change(int amount, vector<int>& coins) {
        int dp[amount+1];
        memset(dp, 0, sizeof(dp)); //初始化数组为0
        dp[0] = 1;
        for (int j = 1; j <= amount; j++){ //枚举金额
            for (int coin : coins){ //枚举硬币
                if (j < coin) continue; // coin不能大于amount
                dp[j] += dp[j-coin];
            }
        }
        return dp[amount];
    }
};
class Solution2 {
public:
    int change(int amount, vector<int>& coins) {
        int dp[amount+1];
        memset(dp, 0, sizeof(dp)); //初始化数组为0
        dp[0] = 1;
        for (int coin : coins){ //枚举硬币
            for (int j = 1; j <= amount; j++){ //枚举金额
                if (j < coin) continue; // coin不能大于amount
                dp[j] += dp[j-coin];
            }
        }
        return dp[amount];
    }
};

如果不仔细看，你会觉得这两个Solution似乎是一模一样的代码，但细心一点你会发现他们在嵌套循环上存在了差异。这个差异使得一个求解结果是排列数，一个求解结果是组合数。

因此在不看后面的分析之前，你能分辨出哪个Solution是得到排列，哪个Solution是得到组合吗？

在揭晓答案之前，让我们先分别用DP的方法解决爬楼梯和零钱兑换II的问题。每个解题步骤都按照DP三部曲，a.定义子问题，b. 定义状态数组，c. 定义状态转移方程。

70. 爬楼梯

问题描述如下:

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

这道题目子问题是，problem(i) = sub(i-1) + sub(i-2), 即求解第i阶楼梯等于求解第i-1阶楼梯和第i-2阶楼梯之和。

状态数组是 DP[i], 状态转移方程是DP[i] = DP[i-1] = DP[i-2]

那么代码也就可以写出来了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int climbStairs(int n) {
        int DP[n+1];
        memset(DP, 0, sizeof(DP));
        DP[0] = 1;
        DP[1] = 1;
        for (int i = 2; i <= n; i++){
            DP[i] = DP[i-1] + DP[i-2] ;
        }
        return DP[n];

    }
};

由于每次我们只关注DP[i-1]和DP[i-2]，所以代码中能把数组替换成2个变量，降低空间复杂度，可以认为是将一维数组降维成点。

如果我们把问题泛化，不再是固定的1，2，而是任意给定台阶数，例如1,2,5呢？

我们只需要修改我们的DP方程DP[i] = DP[i-1] + DP[i-2] + DP[i-5], 也就是DP[i] = DP[i] + DP[i-j] ,j =1,2,5

在原来的基础上，我们的代码可以做这样子修改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int climbStairs(int n) {
        int DP[n+1];
        memset(DP, 0, sizeof(DP));
        DP[0] = 1;
        int steps[2] = {1,2};
        for (int i = 1; i <= n; i++){
            for (int j = 0; j < 2; j++){
                int step = steps[j];
                if ( i < step ) continue;// 台阶少于跨越的步数
                DP[i] = DP[i] + DP[i-step];
            }
        }
        return DP[n];

    }
};

后续修改steps数组，就实现了原来问题的泛化。

那么这个代码是不是看起来很眼熟呢？我们能不能交换内外的循环呢？也就是下面的代码

1
2
3
4
5
6
7
for (int j = 0; j < 2; j++){
    int step = steps[j];
    for (int i = 1; i <= n; i++){
        if ( i < step ) continue;// 台阶少于跨越的步数
         DP[i] = DP[i] + DP[i-step];
    }
}

大家可以尝试思考下这个问题，嵌套循环是否能够调换，调换之后的DP方程的含义有没有改变？

零钱兑换II

问题描述如下:

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

定义子问题: problem(i) = sum( problem(i-j) ), j =1,2,5. 含义为凑成总金额i的硬币组合数等于凑成总金额硬币i-1, i-2, i-5,…的子问题之和。

我们发现这个子问题定义居然和我们之前泛化的爬楼梯问题居然是一样的，那后面的状态数组和状态转移方程也是一样的，所以当前问题的代码可以在之前的泛化爬楼梯问题中进行修改而得。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int dp[amount+1];
        memset(dp, 0, sizeof(dp)); //初始化数组为0
        dp[0] = 1;
        for (int j = 1; j <= amount; j++){ //枚举金额
            for (int i = 0; i < coins.size(): i++){ 
                int coin = coins[i]; //枚举硬币
                if (j < coin) continue; // coin不能大于amount
                dp[j] += dp[j-coin];
            }
        }
        return dp[amount];
    }
};

这就是我们之前的Solution1代码。

但是当你运行之后，却发现这个代码并不正确，得到的结果比预期的大。究其原因，该代码计算的结果是排列数，而不是组合数，也就是代码会把1,2和2,1当做两种情况。但更加根本的原因是我们子问题定义出现了错误。

正确的子问题定义应该是，problem(k,i) = problem(k-1, i) + problem(k, i-k)

即前k个硬币凑齐金额i的组合数等于前k-1个硬币凑齐金额i的组合数加上在原来i-k的基础上使用硬币的组合数。说的更加直白一点，那就是用前k的硬币凑齐金额i，要分为两种情况开率，一种是没有用前k-1个硬币就凑齐了，一种是前面已经凑到了i-k，现在就差第k个硬币了。

状态数组就是DP[k][i], 即前k个硬币凑齐金额i的组合数。

这里不再是一维数组，而是二维数组。第一个维度用于记录当前组合有没有用到硬币k，第二个维度记录现在凑的金额是多少？如果没有第一个维度信息，当我们凑到金额i的时候，我们不知道之前有没有用到硬币k。

因为这是个组合问题，我们不关心硬币使用的顺序，而是硬币有没有被用到。是否使用第k个硬币受到之前情况的影响。

状态转移方程如下

1
2
3
4
if 金额数大于硬币
    DP[k][i] = DP[k-1][i] + DP[k][i-k]
else
    DP[k][i] = DP[k-1][i]

因此正确代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int K = coins.size() + 1;
        int I = amount + 1;
        int DP[K][I];
        //初始化数组
        for (int k = 0; k < K; k++){
            for (int i = 0; i < I; i++){
                DP[k][i] = 0;
            }
        }
        //初始化基本状态
        for (int k = 0; k < coins.size() + 1; k++){
            DP[k][0] = 1;
        }
        for (int k = 1; k <= coins.size() ; k++){
            for (int i = 1; i <= amount; i++){  
                if ( i >= coins[k-1]) {
                    DP[k][i] = DP[k][i-coins[k-1]] + DP[k-1][i]; 
                } else{
                    DP[k][i] = DP[k-1][k];
                }
            }
        }
        return DP[coins.size()][amount];
    }
};

我们初始化的数组大小为coins.size()+1* (amount+1), 这是因为第一列是硬币为0的基本情况。

此时，交换这里面的循环不会影响最终的结果。也就是

1
2
3
4
5
6
7
8
9
for (int i = 1; i <= amount; i++){  
    for (int k = 1; k <= coins.size() ; k++){ 
        if ( i >= coins[k-1]) {
            DP[k][i] = DP[k][i-coins[k-1]] + DP[k-1][i]; 
         } else{
             DP[k][i] = DP[k-1][k];
         }
     }
}

之前爬楼梯问题中，我们将一维数组降维成点。这里问题能不能也试着降低一个维度，只用一个数组进行表示呢？

这个时候，我们就需要重新定义我们的子问题了。

此时的子问题是，对于硬币从0到k，我们必须使用第k个硬币的时候，当前金额的组合数。

因此状态数组DP[i]表示的是对于第k个硬币能凑的组合数

状态转移方程如下

1
DP[[i] = DP[i] + DP[i-k]

于是得到我们开头的第二个Solution。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int dp[amount+1];
        memset(dp, 0, sizeof(dp)); //初始化数组为0
        dp[0] = 1;
        for (int coin : coins){ //枚举硬币
            for (int i = 1; i <= amount; i++){ //枚举金额
                if (i < coin) continue; // coin不能大于amount
                dp[i] += dp[i-coin];
            }
        }
        return dp[amount];
    }
};

好了，继续之前的问题，这里的内外循环能换吗？

显然不能，因为我们这里定义的子问题是，必须选择第k个硬币时，凑成金额i的方案。如果交换了，我们的子问题就变了，那就是对于金额i, 我们选择硬币的方案。

同样的，我们回答之前爬楼梯的留下的问题，原循环结构对应的子问题是，对于楼梯数i, 我们的爬楼梯方案。第二种循环结构则是，固定爬楼梯的顺序，我们爬楼梯的方案。也就是第一种循环下，对于楼梯3，你可以先2再1，或者先1再2，但是对于第二种循环

参考资料

数据结构与算法

LeetCode-045- 跳跃游戏II

跳跃游戏II

https://leetcode-cn.com/problems/jump-game-ii/

相对与之前的跳跃游戏，这道题目保证能够抵达终点，但是要求你输出最短路径。

DP三部曲，定义子问题，定义状态数组，和状态转移方程。

  • 子问题，到i个位置的最短步数，等于0..i-1中能够到i的最小步数+1
  • 状态数组: dp[i]
  • 状态转移方程: dp[i] = min(dp[i],dp[j]+1), j =0..i

下面就是最初版的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 90 / 92 个通过测试用例
class Solution1 {
public:
    int jump(vector<int>& nums) {
        int dp[nums.size()];
        for (int i = 0; i < nums.size(); i++) dp[i] = INT_MAX;
        dp[0] = 0; //初始化第一个位置
        for (int i = 1 ;i < nums.size() ; i++){
            for(int j = 0; j < i ; j++){
                if (nums[j] + j >= i){
                    dp[i] = min(dp[i],dp[j]+1);
                }
            }
        }
        return dp[nums.size()-1];
    }
};

虽然代码正确，也能得到正确的结果，但是超时了，卡在了一个全为1的输入中。

优化下代码：外层依旧遍历整个数组，内层循环则是遍历当前数组能够抵达的位置， 更改其最小步数。

也就是状态转移方程变成了dp[i+j] = min(dp[i+j], dp[i]+1);

这就保证了对于全为1的数组，内层循环只会走一步，就避免了之前的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution2 {
public:
    int jump(vector<int>& nums) {
        int dp[nums.size()];
        int num_len = nums.size() ;
        for (int i = 0; i < nums.size(); i++) dp[i] = INT_MAX;
        dp[0] = 0; //初始化第一个位置

        for (int i = 0 ;i < nums.size() ; i++){
            for(int j = 1; j <= nums[i] ; j++){
                int next = min(i+j, num_len-1); //不能越界
                dp[next] = min(dp[next],dp[i]+1);
            }
        }
        return dp[nums.size()-1];
    }
};

当我满怀信心运行代码的时候，结果还是超时了。

原来输入中，还有一个单调递减的情况，导致最终内层循环次数分别为n,n-1,n-2…1位置，导致许多不必要的运算。

继续优化：我们新增一个变量，farthest，表示每次能够抵达的最远距离。如果不能保证当前位置能够比farthest走的更远的时候, 就说明当前位置不够好。

同时，在内层循环之前，我们先判断当前位置是否能够直接抵达终点，如果可以就直接返回结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int jump(vector<int>& nums) {
        int num_len = nums.size() ;
        if ( num_len <= 1) return 0;
        int farthest = 0;
        int dp[num_len];
        for (int i = 0; i < num_len ; i++) dp[i] = INT_MAX - 1;
        dp[0] = 0; //初始化第一个位置

        for (int i = 0 ;i < num_len ; i++){
            if ((i+nums[i]+1)>= num_len) return dp[i]+1;
            for(int j = 1; j <= nums[i] && nums[i] + i > farthest; j++){
                int next = i + j; //抵达的最后位置
                dp[next] = min(dp[next],dp[i]+1);
            }
            farthest = i + nums[i];
        }
        return dp[num_len-1];
    }
};

继续优化: 我们内层循环每次也不是需要从当前的下一个位置开始更新，而是farthest-i开始，因为next=i+j = i+farthest-i+j = farthest, 即我们从之前所能抵达最远位置开始更新，一直更新到当前所能抵达最远位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int jump(vector<int>& nums) {
        int num_len = nums.size() ;
        if ( num_len <= 1) return 0;
        int farthest = 0;
        int dp[num_len];
        for (int i = 0; i < num_len ; i++) dp[i] = INT_MAX - 1;
        dp[0] = 0; //初始化第一个位置

        for (int i = 0 ;i < num_len ; i++){
            if ((i+nums[i]+1)>= num_len) return dp[i]+1;
            for(int j = farthest - i; j <= nums[i] && nums[i] + i > farthest; j++){
                int next = i + j; //抵达的最后位置
                dp[next] = min(dp[next],dp[i]+1);
            }
            farthest = i + nums[i];
        }
        return dp[num_len-1];
    }
};

最后的代码提交之后运行速度是4ms。

同样是两层循环，通过剪枝能够大大提高运算速度。

数据结构与算法

LeetCode-322-零钱兑换

硬币兑换

来源LeetCode, 题目地址<https://leetcode-cn.com/problems/coin-change/>

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

暴力递归（回溯）

每一种硬币都有选择和不选两种情况，因此最简单的方法就是穷举所有可能性，从中找到最小的选择，递归树如下:

状态树

每次节点的子节点都会出现3个分支，因此时间复杂度是指数级。

尽管明知这个代码是不能通过LeetCode，我还是把代码给写完了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution1 {
public:
    int MIN_COMB = INT_MAX;
    int coinChange(vector<int>& coins, int amount) {
        DFS(0, amount, coins);
        return MIN_COMB;
    }

    void DFS(int depth, int amount, vector<int>& coins){
        if (amount == 0){
            MIN_COMB = min(depth, MIN_COMB);
            return ;
        }
        for (auto coin : coins){
            if (amount - coin < 0 ) continue; //减枝
            DFS(depth+1, amount - coin, coins);
            
        }
        return ;
    }
};

对于一些比较正常的数据，这个代码都能正常运行，但是对于LeetCode中的[186,419,83,408] 6249，标准答案是20，也就是至少有20层，因此计算量至少是3^20，但是递归深度可以达到75层，计算量就是一个天文数字了。

递归的广度优先搜索

递归树其实是一种深度优先的搜索方法，我们可以采用广度优先搜索方法，对递归树按层进行遍历，第一次遇到amount=0的时候，也就是最小的遍历层数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution2 {
public:
    int coinChange(vector<int>& coins, int amount) {

        queue<pair<int,int>> q; //level and amount
        q.push({0, amount});

        while ( !q.empty()) {

            int level = q.front().first;
            int surplus = q.front().second;
            q.pop();

            for (auto c : coins){
                if ( surplus - c < 0 ) continue;
                if ( surplus - c == 0 ) return level + 1;
                q.push({level+1, surplus-c});
            }
        }
        return -1;


    }
};

尽管看起来， BFS或许比DFS能够更快的找到最终的解（不需要遍历所有的状态），但是由于递归树本身就是指数增长，因此只要层数过大，时间就会惊人的增长。

你可以保持[1,2,5]不变，然后依次测试，10,20,50,80,100. 你会发现前4个解决速度都比较快，但是到了100，时间就上天了。

贪心算法

暴力递归的问题在于，节点的增长是指数级别的。如果我们每次都选择当前的最优解，也就是对于11，从1，2，5中找交换的硬币的时候，都以5，2，1这种顺序进行选择，就避免了指数级别的增长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        sort(coins.begin(), coins.end(), std::greater<>());
        return DFS(0, amount, coins);
    }

    int DFS(int level, int amount, vector<int>& coins){
        if (amount <= 0){
            return amount == 0 ? level : -1;
        }
        for (auto coin : coins){
            int res = DFS(level+1, amount - coin, coins);
            if (res > 0 ) return res;
        }
        return -1;
    }
};

但是贪心算法有一个弊端，你得要证明能够从局部最优一直推导出全局最优解，才能保证你的结果是正确的。如果无法保证，那么贪心算法不一定保证最终结果就是最优解，所以这里贪心算法也是无法通过。

递归+记忆化

在我们之前的递归树中，无论采用何种遍历方式（DFS或BFS），都无法逃脱时间指数级别增长的命运。

不过当我们仔细观察递归树的时候，我们会发现一些节点是被重复计算的。如果能避免这些重复计算，那么时间复杂度就会降低到O(n^2)

在原来递归的代码上加上记忆化，我写了很久，主要是不知道在递归的时候，如何记录当前情况下，如何挑选最优子问题。

先放上正确的答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    unordered_map<int, int> dict;
    int coinChange(vector<int>& coins, int amount) {
        if (amount < 1) return 0;
        return DFS(coins, amount);
    }
    int DFS(vector<int>& coins, int amount){
        if (amount < 0 ) return -1;
        if (amount == 0 ) return 0;
        if (dict.find(amount) != dict.end()) return dict[amount];

        int min = INT_MAX; //足够大的值
        for (int coin : coins){
            int res = DFS(coins, amount-coin);
            if (res >= 0 && res < min){
                min = res + 1;
            }
        }
        dict[amount] = (min == INT_MAX ? -1 : min);
        return dict[amount];
    }
};

递归返回的从最后一层到当前层的所需的步数。而之前的递归程代码则是每次记录当前的深度，最终拿深度和全局最小值进行比较。

下面则是我的错误示范。我的代码主题也是想算出最后位置到当前位置的经历的步数，但是我想用最后一层的深度减去当前的深度。结果每一个amount对应都是1.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 递归+记忆化
class Solution4 {
public:
    unordered_map<int, int> dict;
    int coinChange(vector<int>& coins, int amount) {
    
        return DFS(0, amount, coins);
    }

    int DFS(int depth, int amount, vector<int>& coins){
        if (amount == 0){
            return depth;
        }

        if (dict.find(amount) != dict.end() ) {
            return dict[amount];
        }

        int local_min = INT_MAX;

        for (auto coin : coins){
            if (amount - coin < 0 ) continue; 
            local_min = min(local_min, DFS(depth+1, amount - coin, coins) -depth);
            
        }
        dict[amount] = (local_min == INT_MAX ? -1 :   local_min);
        return dict[amount];
    }
};

自底向上的动态规划

事实上递归加记忆化就是一种动态规划，只不过递归是一种自顶向下的策略。并且有了之前递归加记忆化的经验，我们写递推就变得简单了。

第一步: 定义子问题。我们求解组成金额为n的最少硬币数，也就是求解一系列 n-k (k=coins) 子问题中的最小选择加1。以amount=11，coins=1,2,5为例。求解amount=11的最少硬币，也就是在10,9,6这三种选择中挑选其中所需硬币最小的子问题，然后加1.

第二步：定义DP数组. f(n) = min{f(n-k), k = 1,2,5} + 1

第三步: 定义DP方程: dp[i] = min(dp[i], dp[i-coins[j] ] )+ 1

最终代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        int MAX = amount + 1;// 只要保证比amount大即可, 因为后续要和当前最小的选择比较。
        vector<int> dp(amount+1, MAX); //DP数组
        dp[0] = 0;
        for (int i = 1; i <= amount; i++){
            for (int j = 0; j < coins.size(); j++){
                if (coins[j] <= i){ //举例, i = 2, 只能考虑coin=1,2, 排除5
                    dp[i] = min(dp[i], dp[i-coins[j]] + 1); 
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
};

代码中的细节，

  • 初始化的数组大小为amount+1, 不能是amount, 否则只能表示0到amount-1
  • 初始化的数组存放的值，要比最坏情况下的最少硬币数大，例如amount=10, 硬币只有11，那么数组内容就会是原本情况，最终的结果是比amount大，说明无解。因此，MAX = INT_MAX-1 也是可以的。

最终来看，自底向上的动态递归的代码反而是最简洁的。