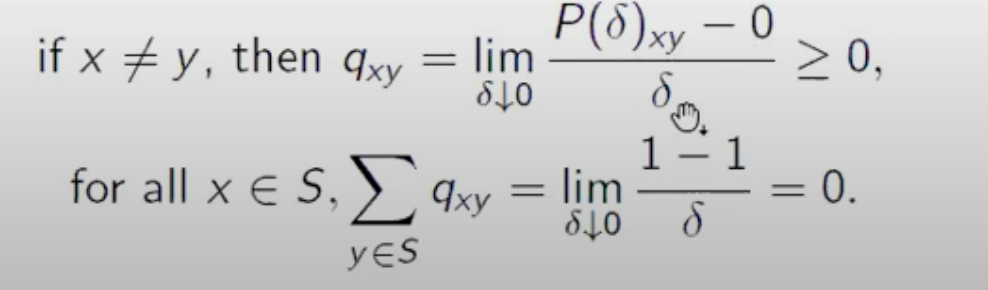MacOS原生Arm64架构的R语言环境配置-简明版

在很早之前，我出过一期视频，介绍过如何在Arm64架构下（即M系列的芯片，包括M1，M2等）的Mac电脑上配置R语言分析环节。当时采用的是intel转译方案。只所以那样子做，是避免在环境配置上浪费不必要的时间，耽误了真正的学习过程。同时，我也写了MacOS原生Arm64架构的R解决依赖编译问题给那些需要折腾的人。

不过，自从R进入了4.2, Bioconductor发布3.16之后，现阶段的M1/M2等用户就可以开始用原生的Arm版本的R了，因为无论是CRAN，还是Bioconductor都提供了预编译的arm版本的R包。

其他

我目前对Web开发的一些认知

最早，我从一个讲解电脑软件知识的杂志上看到的一篇文章，讲的是1元建站，心中植下了也要搞一个网站的想法。在很长一段时间，我都没有系统性的学习过相关知识，就导致我脑中的知识很混杂。不过，当相关知识积累到一定程度时，你可能就会在某一刻顿悟，惊呼，原来是这样！

想要在别人通过互联网访问到你提供的资源，最关键的一步，是需要有一个拥有一个公网IP的服务器。由于早年设计互联网的时候，没有想到会有那么多人上网，于是IP地址非常有限，（特指的IPv4,目前的IPv6暂时不存在这个问题），因此并非所有的机器都拥有可被直接访问的地址，绝大部分都是内网地址。为方便理解，你可以认为服务器的IP地址就如同小区的门牌号码，小区里面有很多楼，因此每个楼还有一个内部编号，好比是内网地址。你住在A小区，告诉一个B小区的人自己在A小区的楼号，那个人在自己小区即便找到了那个楼，那个楼里面也没有你。

为了获取一个独立公网IP的服务器，你有如下几个选择。

  1. 联系你的网络运营商，让他给你家分配一个独立IP；
  2. 购买一台独立的云服务器，然后自己在上面配置环境；
  3. 购买别人搭建好环境的服务器，托管自己的应用。
  4. GitHub Page

独立的云服务器

托管服务器

早年间绝大部分小白建站，都是走的第三条路，自己在本机上用Adobe Dreamweaver这类工具把网站设计好，然后打包资源，将结果上传到对方要求的一个地方。

如果全部是静态资源，目前一个很好的选择就是用GitHub Page免费构建一个网页，然后购买一个域名，将域名解析到GitHub Page对应的地址。

这里提到了两个新的知识点，静态资源和域名。先讲最简单的域名，因为所谓的域名， 无非就是用更好记的单词去替代一串数字。访问域名的时候，会有一个DNS服务器（Domain Name System）帮你做相应的转换。注意，域名的注册是要钱的，好的域名还可以用来交易。

价格不菲的域名

购买后的域名，需要在域名提供商的管理后台设置一个解析，即让域名提供商去告诉其他DNS服务器，域名实际对应的IP地址。

下一部分，我们来讲讲静态资源和动态资源。这两者的区分并不是网页上的元素能不能动，比如说图片的切换（由JavaScrip控制），而是网页返回的内容是不是动态生成的，例如你搜索时，返回的内容就是经过数据库查询后返回给你，你在购物网站搜索商品也是如此。

举个例子：很久之前，我是通过HUGO框架搭建我自己的个人博客。HUGO会将我写好的Markdown文本进行处理，得到可以直接在本地查看的网页，我只要将其上传到服务器某个目录下，或者GitHub Page下，就算部署了我的博客。

目前，我的博客用的是Halo进行建站，它有一套后台管理系统，我在后台编辑文章，编辑好的文章会记录在底层的数据库。用户访问时，会先去进行数据查询，查询的数据返回到前端，进行渲染。

Halo

我们说的Web开发分为两个部分，一部分是别人在浏览器上可以看到的元素（前端），一部分是别人看不到后台处理工作（后端）。

前端开发有3个组成

  • HTML: 控制页面的整体结构，相当于房子的结构
  • CSS: 控制页面的样貌，相当于给房子做装修
  • JavaScript: 控制页面的行为，相当于房子里面的各种开关

后端包括

  • 应用: 不同编程语言开发的工具，用于处理数据，返回结果
  • 应用服务器：负责运行编写的应用。例如Tomcat运行Java的Servlet应用，Python的Django，R的ShinyServer。应用服务器通常会实现一部分HTTP服务器的功能，因此，当网站没有那么大需求时，一个应用服务器就可以了。
  • HTTP服务器: 负责HTTP的响应，获取用户端的请求，将服务端的结果发送给用户端。如Apache，Nginx。相当于应用服务器，HTTP服务器专注于并发，负载均衡。

在Web发展的初期，绝大部分网站都是静态网页，只要把网页写好，放在服务器上就行。但是这样子效率太低了，毕竟对于一个新闻资讯类网站而言，总不可能为条新闻都写一个页面吧。于是，就有了JSP技术，也就是在HTML里面混入Java代码，查询什么数据，就从数据库检索什么数据，填充到HTML指定位置即可。早期，这类数据获取操作每次都要刷新整个页面，在宽带不足的年代，会浪费不少的网页加载时间。另外，这也不利于分工合作，毕竟一个前端开发者未必懂Java（或许他懂PHP），一个Java开发者也未必能处理好HTML，最后出现bug，两方互相甩锅

题外话: R的shiny是可以把HTML,CSS,JS和数据处理逻辑全部混在一个脚本中的。一个简单的应用还好，可能就几百行代码，以一个相对少的代码实现了一个相对好的页面。但是一旦业务复杂起来，动辄上千的代码，混杂了前端的页面展示，后端的数据处理，可能就是灾难。

后来出现了Ajax技术（描述一类动态加载资源的技术），使得前端可以异步的获取数据并且刷新页面（目前不太会写原生的Ajax代码，主要用框架，如Axios），前后端的数据交互基于统一的数据格式（JSON），前端拿到数据后去改变页面上的展示（早年前用JQuery做DOM操作，后来则是AngularJS, Vue，React这类框架）。

如此一来，前后端分离，分工就更加精细了，写网页的只要负责好网页应该怎么展示，我预期从后端拿到什么样的数据，这类数据会如何改变当前的网页，完成开发后把项目部署在网络速度比较快的服务器上。而写后端的人，也不用考虑前端页面怎么展示，专心写数据处理逻辑，把项目部署在性能比较高的服务器上，以便于把要求的内容返回给前端即可。

最后小结一下

  • 公网IP地址是允许公开访问的基础
  • 域名会通过DNS服务商转换成IP地址
  • 静态网站只需要懂HTML/CSS/JS即可
  • 动态网站开发在技术发展前期，会在HTML里混入开发语言的代码。
  • 在后期通过Ajax，让前后端通过JSON交互，前端使用JS改变页面展示。
基因组学

从一则12年前的提问中学习:从配对序列联配到多序列联配

最近学习多基因组比对时，看到一则12年前在Biostars发布的提问, Programming Challange: Pairwise Alignments To Multiple Alignment, 收获颇多，这里记录下。

提问者，一开始阐释了自己的问题，也就是他有10-12个非常近的物种的染色体序列，将这些物种和一个参考染色体比对后，得到了多个结果。他希望，在生成多序列联配结果的同时不影响到原本单独的比对结果。那么，他想的就是，在各个序列中加上一些插入，就可以得到相对基因组的全局联配。

同时，他强调了，自己不是来找序列相似度！他想的是有没有已有的脚本可以做这些事情，或者提供一些代码上的建议帮助他完成。

甚至，他还给了一个案例，来说明自己的需求

也就是把下面这段

1
2
3
4
5
6
7
8
Ref1: CGACAAT--GCACGACAGAGGAAGCAGAACAGATATTTAGATTGCCTCTCATTTTCTCTCCC
Seq1: CGACAATAAGCACGACAGAGGAAGCAGAACAGATA-----ATTGCCTCTCATTTTC-CTCCC

Ref1: CGACAATGCACGACAGAGGAAGC--AGAACAGATATTTAGATTGCCTCTCATTTTCTCTCCC
Seq2: CGACAAT-CACGACAGAGGAAGCTTAGAACAGATATTTAG---GCCTCTCATTTTCTCTCCC

Ref1: CGACAATGCACGACAGAGGAAG----CAGAACAGATATTTAGATTGCCTCTCA----TTTTCTCTCCC
Seq3: CGACAATGCACGACAGAGGAAGTTTTCAGAACAGATATTTAGATTGCCTCTCAAAAATTTTCTCTCCC

变成下面这段。

1
2
3
4
Ref1: CGACAAT--GCACGACAGAGGAAG----C--AGAACAGATATTTAGATTGCCTCTCA----TTTTCTCTCCC
Seq1: CGACAATAAGCACGACAGAGGAAG----C--AGAACAGATA-----ATTGCCTCTCA----TTTTC-CTCCC
Seq2: CGACAAT---CACGACAGAGGAAG----CTTAGAACAGATATTTAG---GCCTCTCA----TTTTCTCTCCC
Seq3: CGACAAT--GCACGACAGAGGAAGTTTTC--AGAACAGATATTTAGATTGCCTCTCAAAAATTTTCTCTCCC

我觉得大部分人看到这样子的提问，就都知道提问者到底需要什么，也就不需要花太多时间思考题目，问提问者更多细节。

排名第一的回答来自于唐海宝老师

他首先回答了，作者需要的工具是TBA/MULTIZ, 可以从Miller Lab下载.

接着补充了一点细节，多序列联配的潜在原则是，gap和insertion的引入和你比对序列的顺序有关。也就是说，在很多情况下，seq1-seq2-seq3和seq2-seq1-seq3`结果是不一样的，“once a gap, always gap”

最后说了TBA软件的不足，即需要用他们定义的MAF格式作为输入，也就是用户得做一些格式转化你工作。并给了一个使用案例

已知参考序列是ref1, 用于比对的序列是seq1, seq2, seq3。比对之后得到ref1.seq1.sing.maf, ref1.seq2.sing.maf, ref1.seq3.sing.maf, 这三个文件。提供一个进化树描述序列的顺序，如(((ref1 seq1) seq2) seq3， 表示ref1和seq1近，后面跟seq2近，最后是seq3。

最后运行如下命令

1
tba "(((ref1 seq1) seq2) seq3)" *.*.maf tba.maf

输出的tba.maf 就是你想要的结果，Good luck!

基因组学

使用jcvi绘制微共线性(Microsynteny)

本文主要介绍如何使用JCVI的synteny子命令基于已有的共线性分析结果，展现局部的共线性。

需要准备的三个输入文件

  • 记录物种内或者物种间的共线性基因对
  • 记录基因坐标的bed文件
  • 布局文件

第一步，基于已有的共线性分析结果(WGDI, MCscan, MCscanX等软件的分析结果），整理出你需要展示的区间的基因对。注意分隔符是制表符，我们保存为blocks.txt

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
AL1G16390	AT1G06380
AL1G16400	AT1G06390
AL1G16410	AT1G06400
AL1G16420	AT1G06410
AL1G16430	AT1G06420
AL1G16440	AT1G06430
AL1G16450	AT1G06440
AL1G16460	AT1G06450
AL1G16470	AT1G06460
AL1G16480	AT1G06470
AL1G16490	AT1G06475
AL1G16510	AT1G06490
AL1G16520	AT1G06500
AL1G16530	AT1G06515
AL1G16540	AT1G06510
AL1G16550	AT1G06520
AL1G16560	AT1G06530
AL1G16570	AT1G06540
AL1G16580	AT1G06550
AL1G16590	AT1G06560
AL1G16600	AT1G06570
AL1G16610	AT1G06580

第二步，整理记录基因坐标的bed文件。bed要求是6列，记录基因的坐标和朝向，第五列填0即可。 我们命名为genes.bed

1
2
3
4
5
6
7
1	3631	5899	AT1G01010	0	+
1	6788	9130	AT1G01020	0	-
...
scaffold_9	1792941	1795545	AL9U12210	0	-
scaffold_9	1796870	1801565	AL9U12220	0	-
scaffold_9	1810180	1812874	AL9U12230	0	+
scaffold_9	1836100	1837535	AL9U12240	0	-

两个要求:

  • 第4列的基因名必须对应共线性对的基因
  • 文件里必须包含你需要展示物种的所有基因（至少是共线性区块的基因）

第三步，提供布局文件, 命名为layout.csv

1
2
3
4
5
# x,  y, rotation,  ha,  va, color, ratio,  label
0.5, 0.4, 0, center,top,  ,  1, A.lyrata Chr1
0.5, 0.3, 0, center, top,  ,  1,  A.thaliana Chr1
# edges
e, 0, 1

该文件分为两个部分：上半部分是track在图中的相对位置(x,y)和旋转角度(rotation)，以及label的对齐方式， ha( left, center, right) va( top, button) 和颜色(color)

下半部分是不同track的共线性关系，e,0,1表示第一个和第二个track有关联。

最后运行程序

1
python -m jcvi.graphics.synteny blocks.txt  genes.bed layout.csv

输出结果为一个pdf，如下所示

micro synteny

因为我们的共线性基因里面是A.lyrata是第一列，所以画图的时候也是A.lyrata在第一行。

案例仅展示了2条序列之间的共线性，实际上jcvi.graphics.synteny是可以展示多条序列的结果，比如说jcvi案例展示graph, peach, cacao三者之间的共线性，提供的两两之间的共线性如下

1
2
3
4
5
6
7
8
9
10
GSVIVT01012261001 . .
GSVIVT01012259001 . .
GSVIVT01012258001 . .
GSVIVT01012257001 . .
GSVIVT01012255001 Prupe.1G290900.1 Thecc1EG011472t1
GSVIVT01012253001 Prupe.1G290800.2 Thecc1EG011473t1
GSVIVT01012252001 Prupe.1G290700.1 Thecc1EG011474t1
GSVIVT01012250001 Prupe.1G290600.1 Thecc1EG011475t1
GSVIVT01012249001 Prupe.1G290500.1 Thecc1EG011478t1
GSVIVT01012248001 Prupe.1G290400.1 Thecc1EG011482t1

通过调整布局(注意布局文件里面的坐标x,y, 以及edge)

1
2
3
4
5
6
7
# x,   y, rotation,     ha,     va, color, ratio,            label
0.5, 0.6,  0, center, top,   ,  1,  grape Chr1
0.3, 0.4, 0, center, bottom,  , .5, peach scaffold_1
0.7, 0.4,  0, center, bottom,   ,   .5, cacao scaffold_2
# edges
e, 0, 1
e, 0, 2

就能输出如下效果的共线性

synteny among three species

参考资料

https://github.com/tanghaibao/jcvi/wiki/MCscan-(Python-version)

如何安装操作系统

读大学的时候，我发现寝室楼下的打印店有一项业务是安装Windows系统，价格估计是80元/次。我非常的纳闷，装系统不是有手就行吗？后来经历的多了，我才知道，装系统，还必须得有一些硬件和软件相关的知识。

基因组学

计算分子进化-搞懂PAML的正选择分析

许多基因组的文章里都会提到使用PAML进行基因的正选择分析(positive selection), 网上也有一些教程介绍如何用PAML进行分析。无论是文章，还是教程，大多只介绍了过程，读完之后，是能够做相应的分析了，但却不知道为什么要这样子做，这篇教程就做这一方面的补充。

我们应该知道组成蛋白序列的氨基酸对应的核苷酸突变可以分为两类，同义置换(synonymous substitution)和非同义置换(nonsynonymous substitution),通过计算非同一置换速率和同义置换速率的比值, omega=dN/dS, 我们可以衡量蛋白的选择压力。如果选择不影响物种适应环境，那么比值两者的速率应该相等，因此比值为1，如果非同义突变会降低物种的适应性，那么dN < dS, 因此比值小于1， 如果非同义突变让提高物种的适应性，那么dN > dS, 则比值大于1. 于是乎，非同义突变率显著高于同义突变即为蛋白质适应性进化的证据。

接下来，我们以书中被子植物光敏色素(phy)的适应性进化作为例子结合理论来讲解，数据方式如下

1
2
3
4
5
6
7
# PAML的安装和配置不再赘述
# codeml的配置文件
wget http://abacus.gene.ucl.ac.uk/ziheng/data/phyACF.codeml.ctl 
# 15个物种的codon联配结果, 包含gap
wget http://abacus.gene.ucl.ac.uk/ziheng/data/phyACF.txt
# 15个物种的系统发育树
wget http://abacus.gene.ucl.ac.uk/ziheng/data/phyACF.trees

下载的配置文件phyACF.codeml.ctl信息显示如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
      seqfile = phyACF.txt
     treefile = phyACF.trees

      outfile = mlc   * main result file name
        noisy = 3 * 0,1,2,3,9: how much rubbish on the screen
      verbose = 0  * 1: detailed output, 0: concise output
      runmode = 0

      seqtype = 1  * 1:codons; 2:AAs; 3:codons-->AAs
    CodonFreq = 2  * 0:1/61 each, 1:F1X4, 2:F3X4, 3:Fcodon
       aaDist = 0  * 0:equal, +:geometric; -:linear, 1-6:G1974,Miyata,c,p,v,a

        model = 2
      NSsites = 2

        icode = 0  * 0:universal code; 1:mammalian mt; 2-10:see below

    fix_kappa = 0  * 1: kappa fixed, 0: kappa to be estimated
        kappa = 5  * initial or fixed kappa
    fix_omega = 0  * 1: omega or omega_1 fixed, 0: estimate
        omega = 0.1

    fix_alpha = 1  * 0: estimate gamma shape parameter; 1: fix it at alpha
        alpha = .0  * initial or fixed alpha, 0:infinity (constant rate)
        ncatG = 3  * # of categories in dG of NSsites models

        clock = 0   * 0:no clock, 1:global clock; 2:local clock; 3:TipDate
        getSE = 0  * 0: don't want them, 1: want S.E.s of estimates
 RateAncestor = 1  * (0,1,2): rates (alpha>0) or ancestral states (1 or 2)

   Small_Diff = .5e-6
*    cleandata = 1  * remove sites with ambiguity data (1:yes, 0:no)?
*        ndata = 3
       method = 0  * 0: simultaneous; 1: one branch at a time

虽然参数很多，但正选择分析上, 我们所需要修改的参数是 model, NSsites, fix_omega, omega 这四项，来决定codeml的分析模式。

首先， 修改配置文件中的 model = 0 和 NSsites = 0. 此时, codeml会计算全局omega.

使用codeml phyACF.codeml.ctl 运行，输出结果在当前目录的mlc文件中。里面信息很多，我们重点关注如下几项

1
2
3
4
5
6
7
8
...
lnL(ntime: 27  np: 29): -29984.121043      +0.000000
...
Detailed output identifying parameters

kappa (ts/tv) =  1.98351

omega (dN/dS) =  0.08975

lnL是似然值(likeilhood value)的自然对数，之所以是负数，是因为计算出似然值是一个非常小的小数，如果不取对数，结果显示就是0，难以使用。

从结果来看，我们算出的全局omega非常小，约为0.09。这很容易理解，因为我们都知道一个蛋白序列，保守的位点肯定远远多于不保守的位点，那么平均下来，整体的值就会很小。因此正选择通常分析的是系统发育关系的特定谱系或者是蛋白质的某几个位点。

接下来，我们修改 model = 2 和 NSsites = 0, 此时codeml会分析我们提供系统发育树中某个分支(foreground)相对于其他分支(background)是否处于正选择。 问题来了，codeml如何判断哪个是foreground，哪些是background呢？此时需要看下 phyACF.trees. 

1
2
3
4
1


((C.Sorg:1.414715, (F.Tom:1.174355, C.Arab:1.734907):0.401510):7.949045 #1, (Oat3:0.217161, (A.Rice:0.255094, (A.Zea:0.084488, A.Sorg:0.041302):0.239315):0.038530):1.329584, ((A1.Pea1:0.304507, A.Soy:0.370169):0.329161, ((A.Pars:0.912283, (A.Tob:0.154040, (A.Tom:0.051204, A.Pot:0.054514):0.100673):0.456387):0.182221, (A.Zuc:0.729785, A.Arab:0.792669):0.136483):0.130833):0.547791);

我们可以使用iTOL这个网页工具对这个树进行展示，树形如下。

iTol of tree

不难从图中发现，有一个明显和其他格格不入的分支，其中包含C. Sorg(高粱,PhyC)和 C.Arab(拟南芥,PhyC), F.Tom(番茄,PhyF)。我们想要检验这一支，是不是受到了正选择。 为了强调这一支，我们需要在树结构对应的位置上加上#1，表示foreground, 而这在我们下载的.tree文件中已经有了，你可以检查下。

我们运行codeml phyACF.codeml.ctl，关注输出文件mlc里的如下内容

1
2
3
4
5
6
7
8
9
...
lnL(ntime: 27  np: 30): -29983.513876      +0.000000
...
Detailed output identifying parameters

kappa (ts/tv) =  1.99551

w (dN/dS) for branches:  0.08998 0.03881

在dN/dS这一行有两个omega值，第一个是background, 第二个是foreground。虽然后者比前者大，但是也没有超过1。另外，似然比检验(LRT)也显示，这两个模式没有明显差异。

这里，我们提到了似然比检验(likelihood-ratio test, LRT), 这个概念很重要，我们需要稍稍展开说明下。它指的是，根据两个竞争的统计模型的似然值的比值，评估两者的拟合度，其中一个是最大化整个参数空间，另一个则是做一些限制。如果限制条件（零假设）被观测数据所支持，那么两者的似然值的差异不会超过抽样误差。因此，LRT检验的是，比值是不是和1有显著区别，或者说比值的自然对数和0有显著区别。

通常似然比检验的统计量表现为两个对数似然值的差值

$$
\lambda_{\mathrm{LR}}=-2\left[\ell\left(\theta_{0}\right)-\ell(\hat{\theta})\right]
$$

这个统计量，我们可以使用卡方检验(chi2)来分析它的显著性。

1
2
3
4
5
# 用R算出
abs(-2*(-29983.513876 - -29984.121043))
# PAML计算chi2, 自由度设置见最后的补充
chi2 1 1.27
df =  1  prob = 0.270475480 = 2.705e-01

对比我们model=2和model=0, 显著性0.27 > 0.05, 不足以拒绝零假设，即我们检测分支的omega相对于全局的omege没有明显差异。

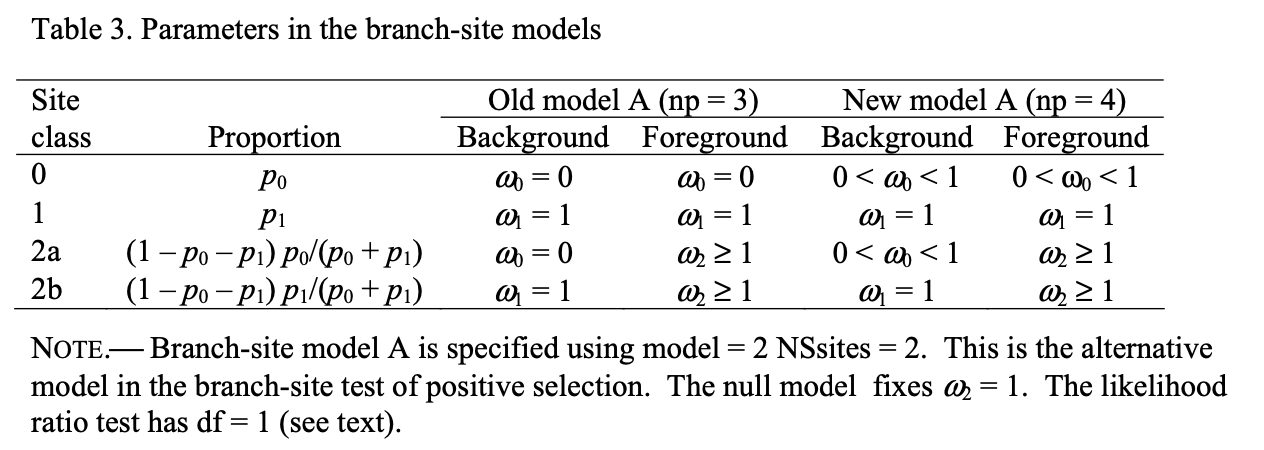
接下来，我们来介绍在所有教程都会提到的branch-site model. 也就是设置model=2 NSsites=2. 它会分析目标分支里的位点是不是受到了正选择。

我们需要建立两个假设，分别是零假设和备择假设

  • 零假设: 检验的分支里的位点不受选择，我们设置参数fix_omega=1, omega = 1
  • 备择假设: 检验的分支里的位点受到正选择，我们设置fix_omege=0, omege = 1.1

在零假设时，输出结果的内容如下，记录lnL= -29704.738847 

1
2
3
4
5
6
7
8
9
10
11
12
13
lnL(ntime: 27  np: 31): -29704.738847      +0.000000
...
Detailed output identifying parameters

kappa (ts/tv) =  2.16177

MLEs of dN/dS (w) for site classes (K=4)

site class             0        1       2a       2b
proportion       0.77433  0.07298  0.13953  0.01315
background w     0.07767  1.00000  0.07767  1.00000
foreground w     0.07767  1.00000  1.00000  1.00000
...

在备择假设时，输出结果的内容如下，记录lnL= -29694.784206

1
2
3
4
5
6
7
8
9
10
11
12
13
14
lnL(ntime: 27  np: 31): -29694.784206      +0.000000

...
Detailed output identifying parameters

kappa (ts/tv) =  2.18201

MLEs of dN/dS (w) for site classes (K=4)

site class             0        1       2a       2b
proportion       0.81323  0.07539  0.10194  0.00945
background w     0.07958  1.00000  0.07958  1.00000
foreground w     0.07958  1.00000 17.59530 17.59530

计算统计量

1
2
abs(-2 *(-29694.784206 - -29704.738847 ) )
# 19.90928

卡方检验(关于自由度是1, 见最后的补充)

1
2
chi2 1 19.9
df =  1  prob = 0.000008160 = 8.160e-06

p远远小于0.01, 为正选择提供了强有力的证据。此时检查mlc输出文件的如下内容，我们还能够确定被选择的位点有哪些。 *表示显著性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Bayes Empirical Bayes (BEB) analysis (Yang, Wong & Nielsen 2005. Mol. Biol. Evol. 22:1107-1118)
Positive sites for foreground lineages Prob(w>1):
    17 T 0.539
    33 G 0.634
    34 D 0.672
    35 S 0.750
    43 E 0.621
    55 R 0.982*
    61 I 0.643
    66 H 0.924
    71 K 0.701
   102 T 0.974*
   104 V 0.932
   105 S 0.994**
   115 D 0.875
   117 P 0.990*
   120 G 0.819
   130 T 0.976*
....

最后补充下为什么自由度是1, 一方面这是PAML的文档中提到的。。

image.png

另一方面，根据定义，自由度指的是统计量计算时不受限制的变量个数。在我们检验分支的时候，只有一个foreground w是需要自由，所以df=1; 在我们对比branch-sites model时，备择假设相对零假设，只有一个w2是自由(fix_omega = 0), 所以df=1

以上是我在学习正选择分析时的整理结果，由于数学功底太弱，有些疑问我还没有结果，比如说似然值为什么那么小？ML模型参数是如何确定的？输出结果中Bayes Empirical Bayes是怎么运算的？这些还需要不断的学习。

如果你并不怎么关注原理的话，可以考虑直接使用一个现有的流程 https://github.com/lauguma/GWideCodeML/wiki

基因组学

计算分子进化-学习笔记2

两个序列之间的距离，定义为平均每个核苷酸置换的期望数。

计算距离是最简单的思路就是看两个序列的相异度，也就是不同的核苷酸占整体的比例. 然而这种思路只能处理高度相似的情况 > 95%, 因为序列在进化过程中，存在反复横跳的情况，也就是 A->T->A, 或者A->T->C->G->A, 也就是核苷酸很有可能经历了多次置换.

为了描述这种状态，我们需要用到马尔科夫链，它是一种随机过程，当前的状态(state)只取决于上一个状态(state), 和更早的状态无关。用公式化的语言，表述如下

$$
P(X=x_n|X=x_{n-1},X=x_{n-2},…) =P(X=X_n|X=x_{n-1})
$$

在书的1.2节中, 作者从开始最简单的JC69模型开始介绍距离估计中的马尔科夫模型。 在书中，作者引入了一个置换率矩阵(subsitution-rate matrix)的概念，并说道 「这里，核苷酸按T, C, A和G的顺序，矩阵的每一行总和为0，任意一个核苷酸i的总置换率为 3$\lambda$, 记为$-q_{ii}$.

刚开始读这段的时候，没有觉得不对劲，仿佛我都看懂了一样。但是，再次阅读到这里的时候，我脑中就闪现一个问题，为什么每一行总和要是0？谁规定的呢？

为了解决这个问题，我就检索了 substituion-rate matrix 这个关键词。但是结果要么是BLOSUM这种替换频率矩阵，要么就返回JC69模型的置换矩阵。

进一步，我想这个概念是不是来自于马尔科夫链。于是我搜索了中文和英文，得到矩阵都是概率转换矩阵(transition matrix)，行和是1，而不是0.

不过山重水复疑无路，柳暗花明又一村，在我查到这篇文章时Nucleotide substitution models，我觉得这篇文章写的特别好，进一步，我发现了这个网站还发布了其他教程，其中一篇就是Understanding Continuous-Time Markov Models, 我终于明白原来书里的马尔科夫链指的是Continuous-time Markov chain, CTMC, 而我之前脑中的马尔科夫链是一个离散过程(DTMC)。

随后，我去找了相关的视频，比较详细的是Lecture 4: Continuous time Markov chains, 如下是我总结的一些知识点

  • CTMC和DTMC一样，定义是当前时刻的状态只受前一刻时间的影响，同时后续讨论的CTMC还要求时间同质，即只要间隔时间相同，转移概率矩阵也相同
  • DTMC只需要一个概率转移矩阵，但是CTMC得要无限个，因为有无数种可能的时间间隔
  • 那么CTMC能否只通过一个矩阵描述呢？基于Chapman-Kolmogorov theorm和矩阵线性微分返程求解，发现可以通过rate matrix(Q)来算出任一时间间隔的转移概率, 即P(t)=exp(Qt)。 Q也可以称之为generator matrix.
  • Q中的元素q_xy表示从x变成y所需要的速率。
  • Q的性质1,根据q_xy的定义, 当x!=y时, q_xy >= 0, 否则会算出负数概率
  • Q的性质2,计算Q矩阵的行和为0, 因此q_xx 为负。

两个性质

计算分子进化这本书涉及到的数学基础有点多，看来要恶补了。

基因组学

计算分子进化-学习笔记1

最近做了些分子进化相关的分析，为了保证自己分析相对靠谱些，因此找了杨子恒编写的【计算分子进化】学习。

成对序列比较的距离估计被反复发现，关键点是，马尔科夫链， 核苷酸之间的置换速率，不同位置的置换速率。估算距离的几类模型

  • 先预设模型，然后使用伽马分布考虑不同位置的置换率
  • 极大似然估计
  • 广义时间可逆模型(GTR/REV)

并不是越复杂的模型效果越好。尤其是当序列间的差异过大时(>40%), 结果会更容易受到模型参数影响。

系统发育重建主要分为两大类，一类是先成对计算序列间距离，构建距离矩阵，然后建树，如简约法； 一类是基于序列的性状（氨基酸，核苷酸）来构树，使得所有物种的所有点都符合树的形状，如极大似然法，贝叶斯法。

物种分歧时间估算的理论基础是分子钟。基本假设是两条序列的差异随着分歧时间线性增加，当有外部校准信息时，可以将序列间的距离或者枝长转换为分歧时间。

Python

放弃conda拥抱mamba

最早conda是Anaconda提供的包管理工具，用于管理python相关库，以及安装一些和Python相关的C/C++环境。

既然C/C++环境能够配置，那么Java, Fortran, JavaScript等编程语言应该也可以支持，于是conda能够管理的软件包变得越发的多。尤其是社区引导的开源项目conda-forge的出现，几乎市面上所有开源工具都可以通过conda进行管理。

但一个可怕的问题也随之而来，那就是原本的包管理工具conda执行速度实在是太慢了，无法处理那么庞大的依赖环境。尤其是当我想去安装一个生物信息学的分析流程时(conda create -c conda-forge -c bioconda -n EDTA EDTA)，conda的安装界面转了一个晚上都没能处理完。为了处理这一危机，mamba孕育而生。它始于2019年，由Wolf Vollprecht开发，拥有和conda完全一样的使用体验，你完全可以用 alias conda=mamba 让mamba作为conda的别名。虽然使用方法完全一样，但是在速度上，mamba则是远超自己的前辈，还是以之前的EDTA安装为例，mamba只需要不到1分钟就可以完成依赖环境的解析，同时它还支持异步下载安装，使得整体速度都有一个质的飞跃。

那么问题来了，如何才能安装配置mamba呢？这里有两个方法。

当你已经安装了miniconda或者anaconda时，我们可以通过conda管理工具去安装, 即 conda install -c conda-forge -n base mamba

如果是在一台全新的服务器上准备安装conda，那么我建议直接配置miniforge作为miniconda的替代。例如下面的代码用于安装mamba作为包管理工具, PyPy3.7作为解释器conda环境。

1
2
wget https://github.com/conda-forge/miniforge/releases/latest/download/Mambaforge-pypy3-Linux-x86_64.sh
bash Mambaforge-pypy3-Linux-x86_64.sh

为什么要用miniforge而不用原来的miniconda呢？主要原因是miniforge会默认配置好conda-forge这个channel, 有些生物信息学软件依赖的包来自于conda-forge而非默认channel。如果没有这个默认配置，可能安装的软件还不能用，例如samtools.

学习Python的面向对象编程心得

众所周知，python是一门面向对象编程的编程语言。但是，我那么多年来基本就用python写些基础脚本，都是调用别人写的函数或者类，顶多自己写几个函数，压根就没用到类。但是，今年(2022)受疫情影响在宿舍里待了2个月，我就逼迫自己用上python的类去改写自己以前写的一些工具，现如今终于能够在自己代码中用到了。

一开始，我是觉得所有代码都可以改成类，无论是否必要。

后来，我终于认清了类，就是数据和相应代码的组织形式