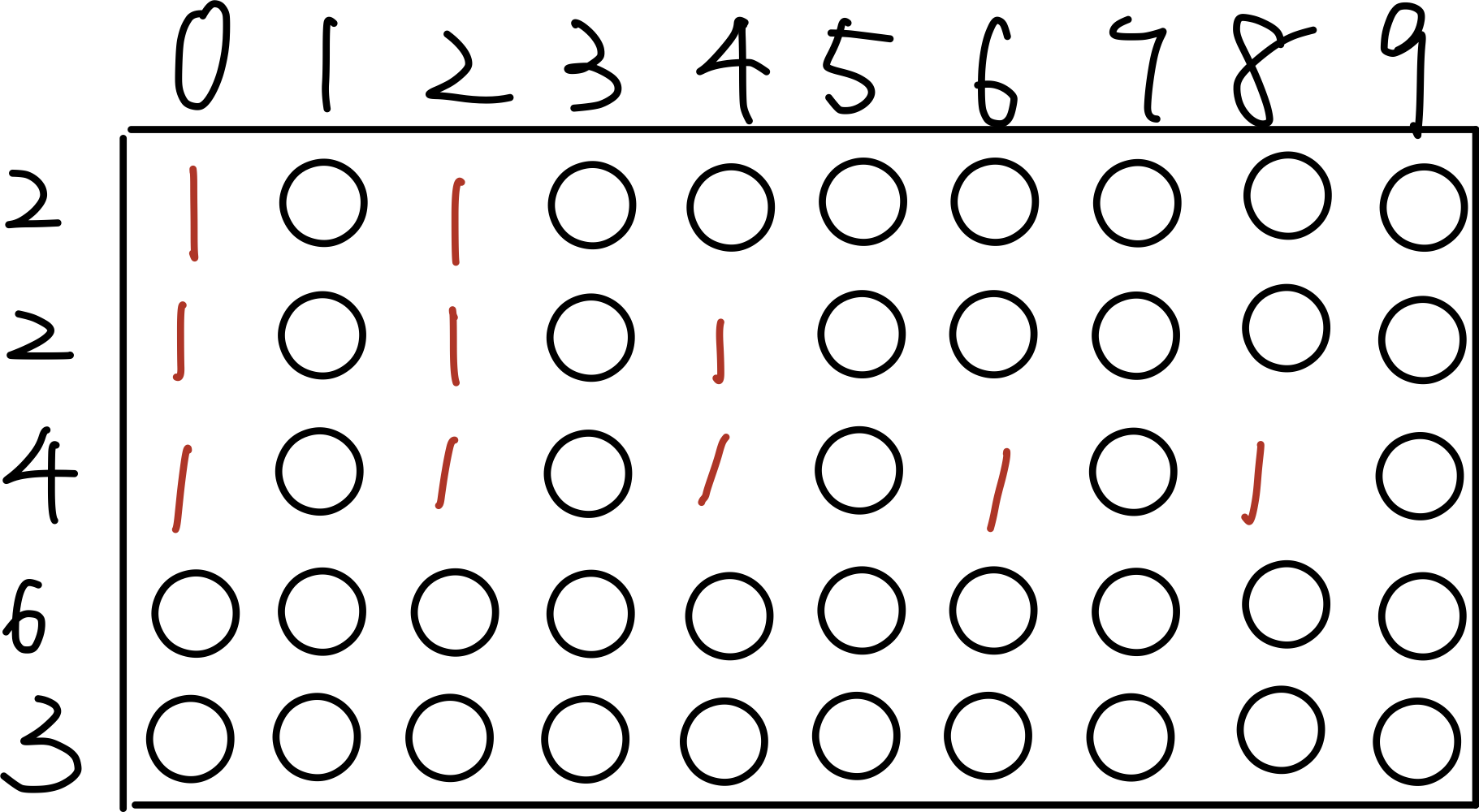数据结构与算法

0-1背包问题

对于一组不同重量、不可分割的物品，我们需要选择一些装入背包，在满足背包最大重量限制前提下，背包中物品总重量的最大值是多少？假设此时是5个物品，2，2，4，6，3，然后背包最大承载两是9.

假如我们使用回溯算法解决该问题, 代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int maxW = 0; //最大重量
int n = 5; //物品数目
int w = 9; // 背包最大重量
int weight[] = {2,2,4,6,3};// 物品重量,2,2,4,6,3

void rucksack(int i, int cw)
{
    if ( cw == w || i == n ){
        if ( cw > maxW ) maxW= w;
        return ;
    }
    rucksack(i + 1, cw);//不装第i个物品
    if ( cw + weight[i] <= w){ //如果装的下
        rucksack(i + 1, cw + weight[i]);
    }
}

如果将代码执行过程产生状态画成树，我们可以发现对于不加入物品2的选择f(1,0)和加入物品2的选择f(1,2), 在下一个选择时，他们有一个相同的状态，f(2,2)。

递归树

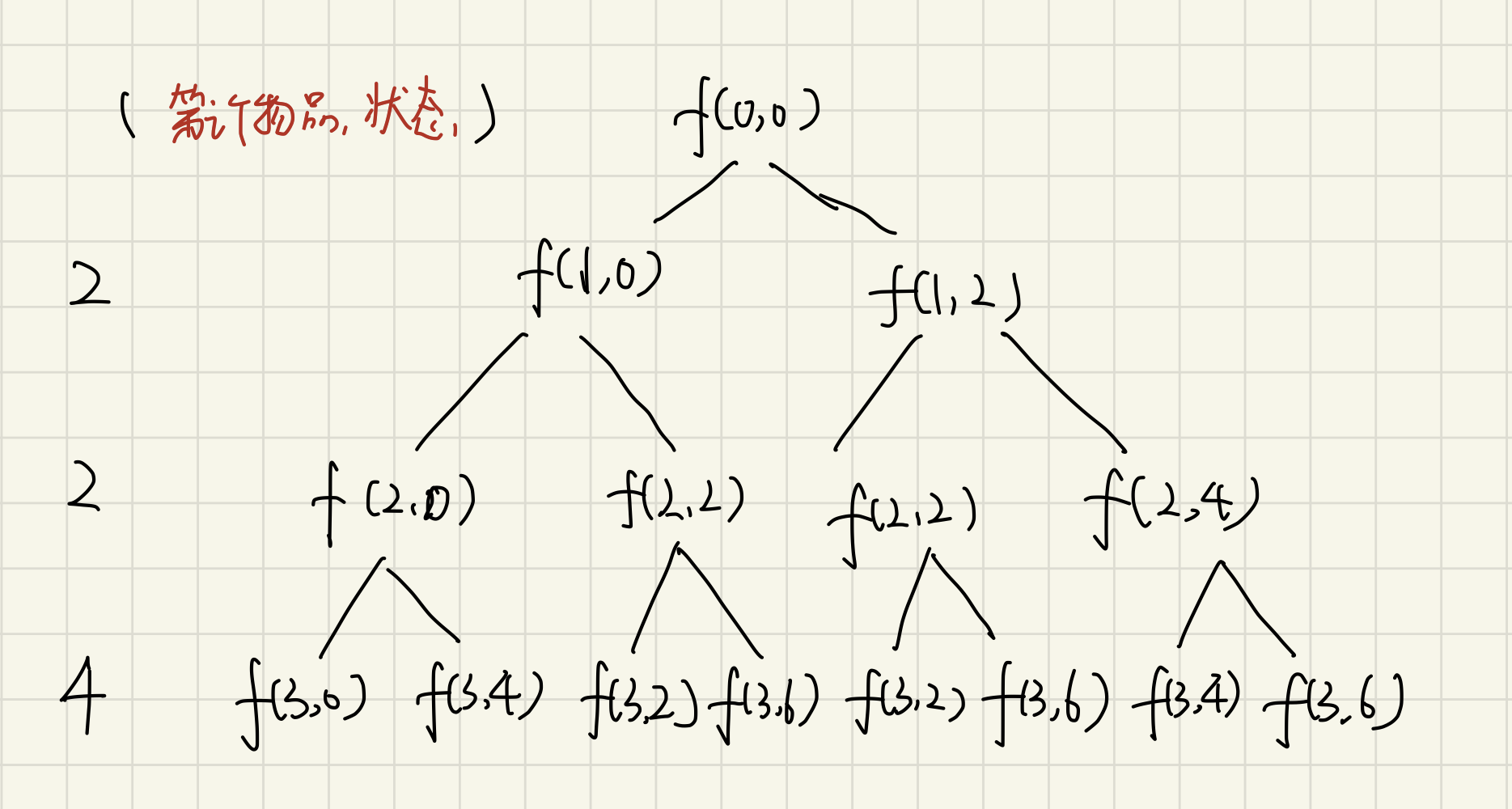
虽然得到它的过程不同，但是从这往后，大家都是一样的。如同你走迷宫，走到一个地方，你发现墙上有一张纸写着，”此路不通”，你就可以不用白费力气去探索了。因此，如果一个问题解决时存在重复子问题，我们可以通过记忆化的方式，避免重复运算，提高计算效率。

从动态规划的角度，我们可以将整个求解过程分为n个阶段，每个阶段都需要决策是否需要将物品放到背包中。每个物品的决策后，背包中物品的重量就有会有种情况，也就是达到了不同的状态，也就是递归树中的不同节点。在每一个层中，我们只记录不同的状态（比如说上图的第2层的两个f(2,2)就可以合并成一种情况，当然第四层就更多了）。这样一来，我们就保证了每一层的状态数就不会超过w个（w是背包的承载重量）。这种合并操作就可以认为是一种记忆化。

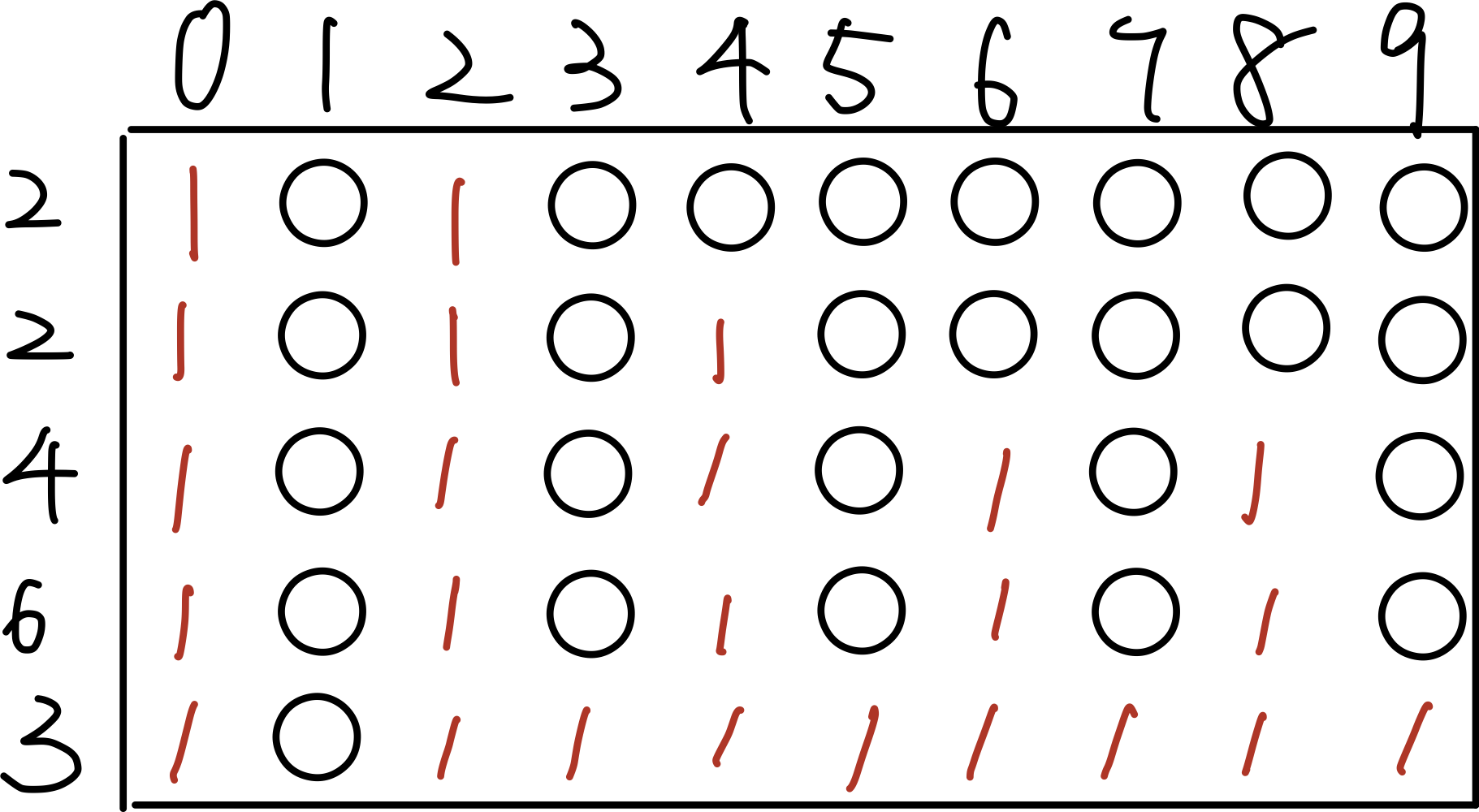
我们先用一个二维数组来记录每层可以达到的不同状态

初始状态

考场重量为2的物品后，会出现两种状态，0和2。

状态1

在上一个状态的基础再考察一个重量为2的物品，会有三种状态，一直不选择，先不选再选2，两次都选2.

状态2

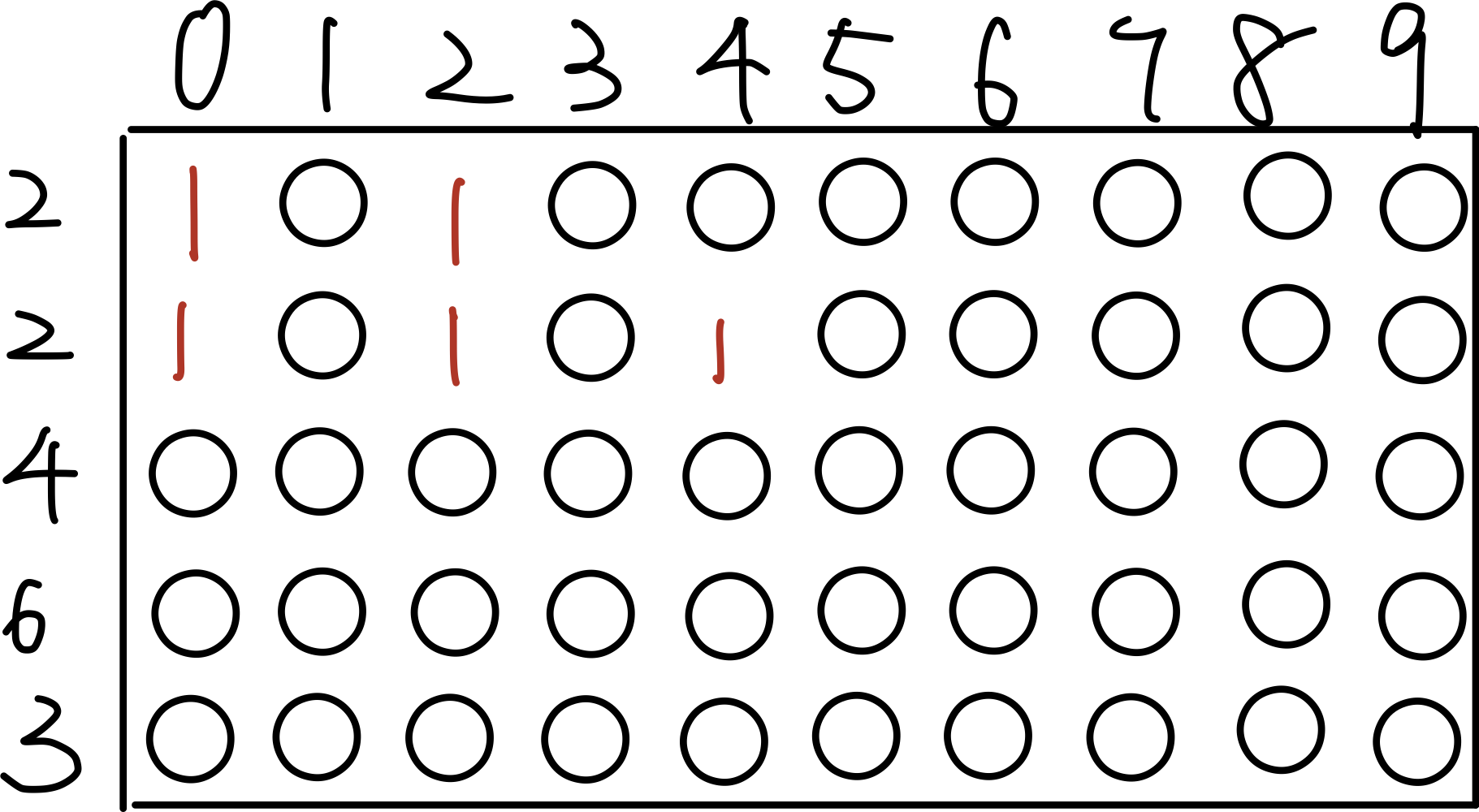
继续考察重量为4的情况时，会出现五种情况，其中重量为4可能来源是0+0+4，2+2+0，这种重复状态就被合并成一种状态，因此减少了计算量。

状态3

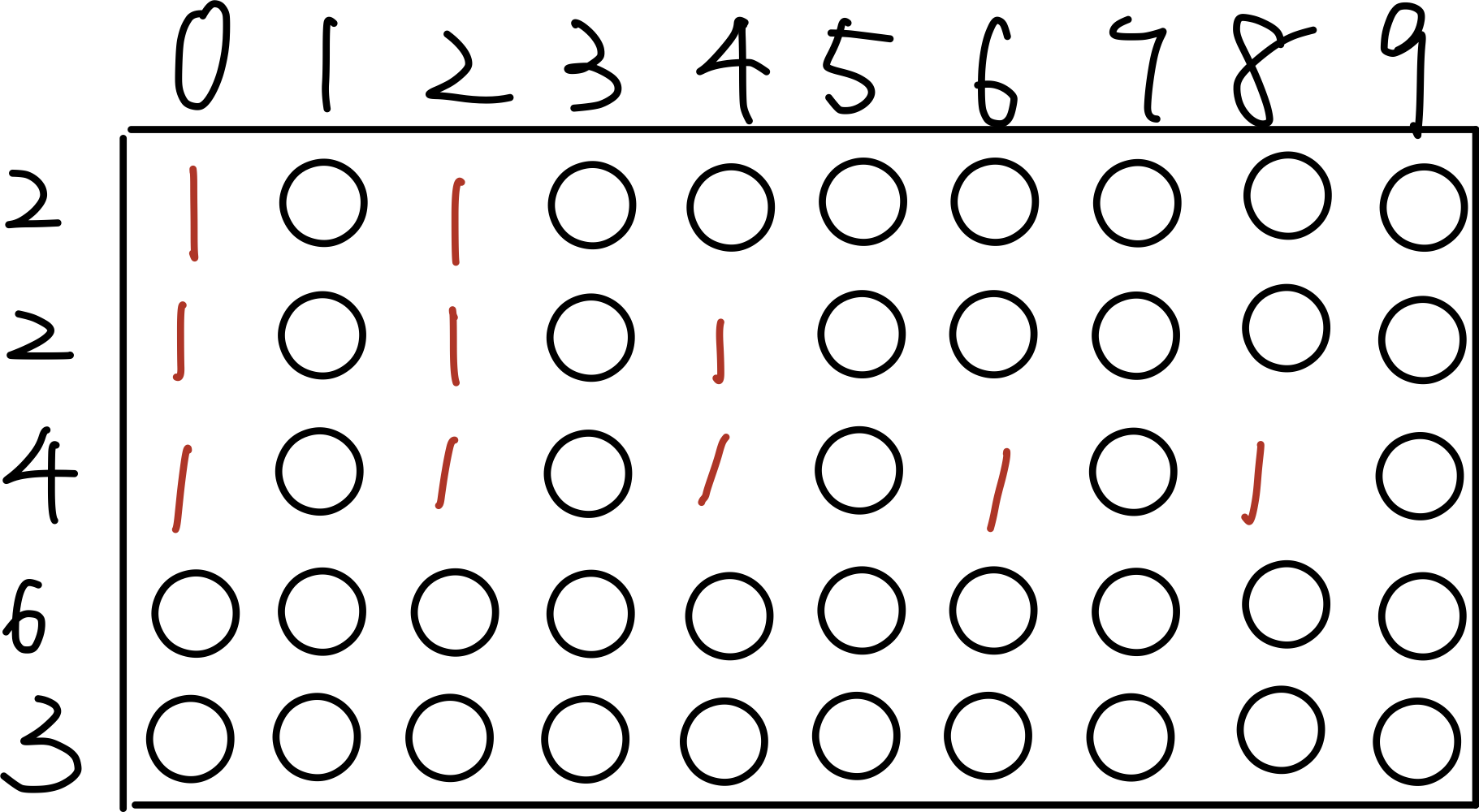
最终状态如下

最终状态

将上面的思考过程翻译成代码就是，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int rucksackDp(int *weight, int num, int w)
{
    //先定义一个二维数组
    int **status = (int **)malloc( sizeof(int *) * num);
    //初始化数组
    for (int i = 0; i < num; i++){
        status[i] = (int *)calloc( w+1, sizeof(int));
    }
    //初始化第一行的值
    status[0][0] = 1; //不放
    if ( weight[0] < w){
        status[0][weight[0]] = 1; //放
    }
    //从第二个开始考虑
    for (int i = 1; i < num; i++){
        //不放的情况，直接将上面的结果复制给当前
        for (int j = 0; j <= w; j++){
            if (status[i-1][j] == 1)  status[i][j] = status[i-1][j];
        }
        //上面循环可以写成
        //memcpy(status[i], status[i-1], sizeof(int) * num);
        //放: 在上一个状态基础上, 将增加后的重量对应位置设置为1
        for ( int j = 0; j <= w -weight[i]; j++){
            if ( status[i-1][j] == 1) status[i][j+weight[i]] = 1;
        }
    }
    //输出结果
    for ( int i = w; i >= 0; --i){
        if (status[n-1][i] == 1) return i;
    }
    return 0;
}

上面我们使用的是二维数组用于保存所有状态，但实际上这里我们只需要一维数组维护前一个状态就可以推导出当前结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int rucksackDp2(int *weight, int num, int w)
{
    //先定义数组
    int *status = (int *)calloc( num, sizeof(int )  );

    //初始化第一行的值
    status[0]= 1; //不放
    if ( weight[0] < w){
        status[weight[0]] = 1; //放
    }
    //从第二个开始考虑
    for (int i = 1; i < num; i++){
        //不放: 保持状态不变
        //放: 在上一个状态基础上, 将增加后的重量对应位置设置为1
        for ( int j = 0; j <= w -weight[i]; j++){
            if ( status[j] == 1) status[j+weight[i]] = 1;
        }
    }
    //输出结果
    for ( int i = w; i >= 0; --i){
        if (status[i] == 1) return i;
    }
    return 0;
}

写动态规划代码的关键在于状态定义和状态转移方程。在0-1背包问题中，我们定义的状态是status[i]就是当前决策结束后到达的重量，而转移方程就是if ( status[j] == 1) status[j+weight[i]] = 1;