数据结构与算法

数据结构之堆(heap)

极客时间的「数据结构与算法之美」的学习笔记，图片来源于「28 | 堆和堆排序：为什么说堆排序没有快速排序快？」

堆满足两个要求:

  1. 完全二叉树
  2. 父节点的元素大于(或小于)子节点的元素

堆的实现

为了实现一个堆，我们需要创造一个堆的数据结构，以及实现堆的插入和删除等操作函数。

堆的存储

由于堆是完全二叉树，因此可以用数组存放堆。第i个节点就放在数组的第i个位置上。它的左子节点是 2i, 它的右子节点是2i+1, 它的父节点是i/2.

堆的存放

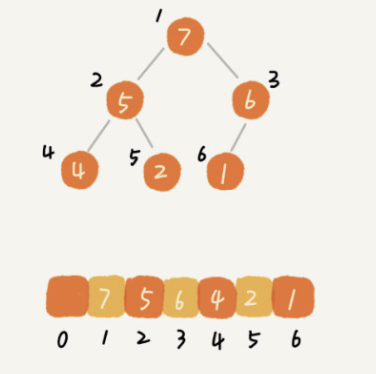
这里定义了一个堆的结构，包含三个元素

1
2
3
4
5
typedef struct _heap {
    int *heap; //指向存放堆对数组
    int n; //堆的大小
    int count; //堆目前的元素
} heap;

创建堆的函数一开始写的代码如下

1
2
3
4
5
6
7
8
9
heap*
createHeap(int n){

    heap *h;
    h->heap = (int*)malloc( sizeof(int) * (n+1));
    h->n = n;
    h->count = 0;
    return h;
}

代码运行会出错，因为heap *h只是声明了一个变量，并没有分配一个内存空间用于构造一个heap结构，同时将h指向这个内存地址。 因此应该加一句,h = (heap*)malloc( sizeof(heap) );. 也就是

1
2
3
4
5
6
7
8
9
10
heap*
createHeap(int n){

	heap *h;
	h = (heap*)malloc( sizeof(heap) );
	h->heap = (int*)malloc( sizeof(int) * (n+1));
	h->n = n;
	h->count = 0;
	return h;
}

堆的操作

堆有两个最常用堆操作，插入元素和删除顶部元素。无论是何种操作，都需要保证操作之后的数据依旧满足堆的两个特性，也就是堆化(heapify)。

每次往堆里加入一个元素，其实是放在数据的最后一个位置，然后让加入元素继续满足堆的性质。

堆的插入

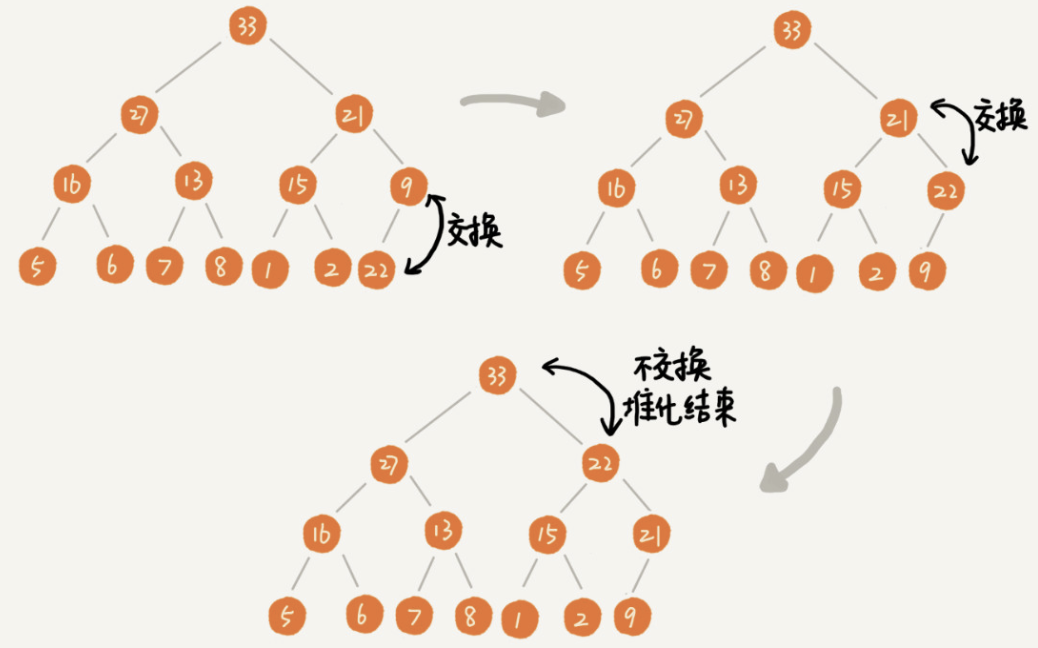
最开始写的插入代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void
insertElement(heap *h, int e){
    if (h->n >= h->count) return;

    // 在数组最后加入新的元素
    int *heap = h->heap;
    int count = h->count;
    heap[++count] = e;

    printf("Insert %d at %d\n", e,count+1);
    h->count = count;

    int i = count;// 数组索引
    //堆化,
    while( (i/2) > 0 && heap[i] > heap[i/2] ){
        swap(heap, i, i /2); //交换父子节点
    }
}

上面代码在调试的时候发现，函数没有输出”Insert %d at %d\n”这一不会显示，也就是说前面的if语句就无法顺利运行。仔细检查发现是逻辑语句写反了, 应该是(h->count >= h->n)。更改此处错误之后，发现堆化依旧失败，原因是while语句中，每次循环中缺少一句i=i/2，导致循环之后结果不正确。

删除堆顶元素有两种方式。一种是直接删除第一个元素，然后开始堆化，但是写代码比较复杂，很可能产生一个非完全二叉树。第二个方式是删除第一个元素，并用最后一个元素替换。然后至上而下进行堆化

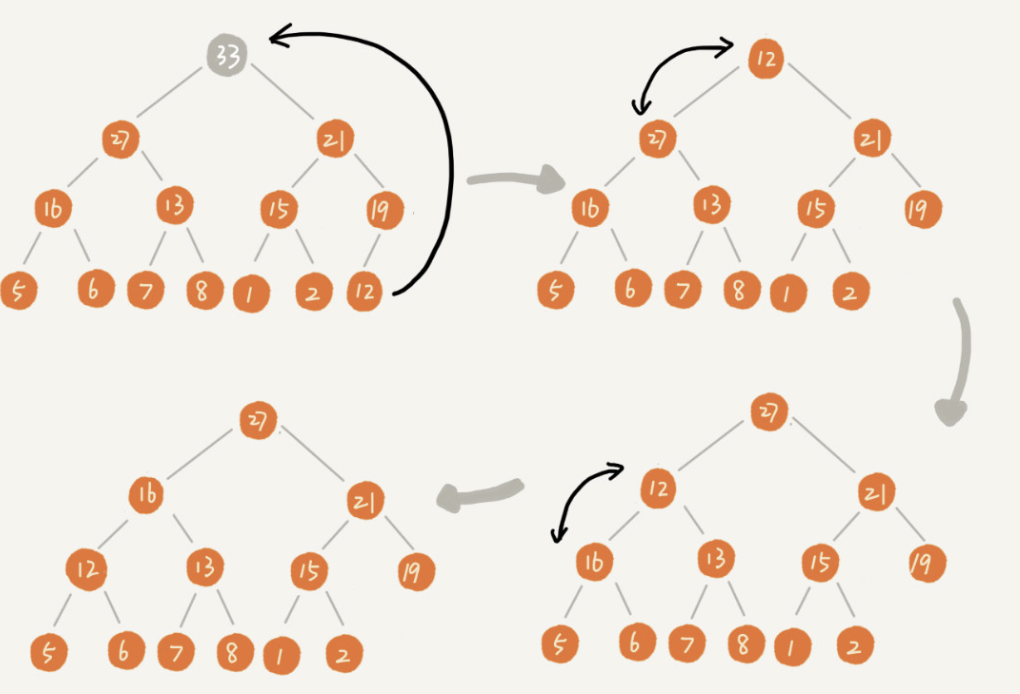
堆的删除操作

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void removeTop(heap *h){

	if (h->count < 1) return ;

	int count = h->count;
	int *heap = h->heap;
	//用最后一个元素替代第一个元素
	heap[1] = heap[count];
	//删除最后一个元素
	h->count = --count;
	// 自上而下堆化
	int i = 1;
	while ( true ){
	    int max_pos = i;
		if ( i*2 <=count && heap[i] < heap[i*2]) max_pos = i*2; //和左子节点比较
		if ( i*2+1<=count && heap[i] < heap[i*2+1]) max_pos = i*2+1; //和右子节点比较
		if (max_pos == i) break; // 不再发生交换, 当前位置就是最大位置
		swap(heap, i, max_pos); //将当前节点和子节点进行交换
		i = max_pos ; //将i设置为子节点的索引
	}

}

最后代码参考https://github.com/xuzhougeng/learn-algo/blob/master/heap.c