线性代数学习笔记-利用最小二乘法做线性回归

背景知识

在学习线性代数的时候，我们都会先从线性方程组入手。求解一个线性方程组是否存在解，如果存在解，那么有多少解，比方说求解下面这个方程组

$$
x_1 - 2x_2 = -1
$$
$$
-x1 - 2x_2 = 3
$$

先别急着掏出纸和笔进行运算。在线性代数中, 这类线性方程组更常见的表述方式为
$$
Ax = b
$$
其中，A是系数矩阵，x和b都是向量。在R语言中，这个方程组可以通过solve函数求解

A <- matrix(c(1,-1,-2,-2), ncol = 2)
b <- c(-1,3)
solve(A,b) 
# -2.0 -0.5

如果方程组有解或者无数解，那么我们称方程组是相容的，反之则是不相容。

对于不相容的方程，我们无法求解出一个x使得等式成立，也就是下图的Ax和b不在一个平面上。因此只能找到一个x，让Ax尽可能b和接近，即求解一个x使得$||Ax-b||$最小。也就是$||Ax-b||^2$最小, 也就是$(Ax-b)\cdot(Ax-b)$最小， 这也就是术语最小二乘法( least squares method, 也称之为最小平方法 )的来源。

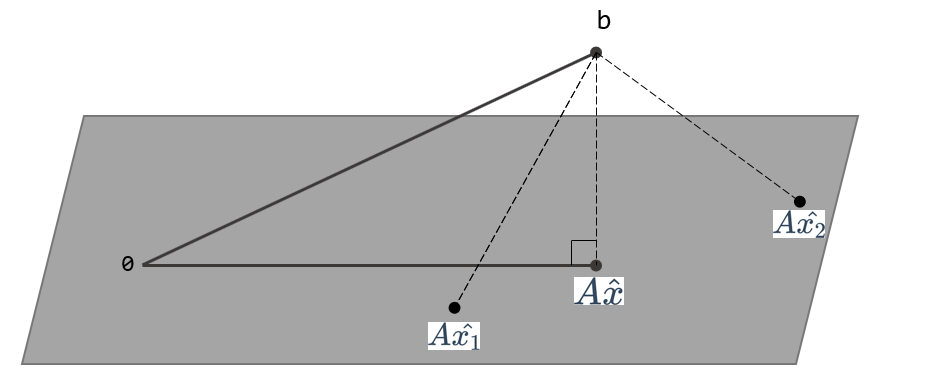
那么如何求解出x呢？跳过教科书的证明部分，这里直接提供定理，用于判定在什么条件下，方程$Ax=b$的最小二乘解是唯一的。

如果已知A的列是线性无关，那么对于方程$Ax=b$，取$A=QR$， 那么唯一的最小二乘解为$\hat x = R^{-1}Q^Tb$,

$A=QR$称之为QR分解，也就是将 $m \times n$ 矩阵A分解为两个矩阵相乘的形式。其中Q是 $m \times n$ 矩阵，其列形成$Col\ A$的一个标准正交基，R是一个 $n \times n$ 上三角可逆矩阵且在对角线元素为正数。

最小二乘直线

那么最小二乘有什么用呢？为了方便讨论实际的应用问题，我们用科学和工程数据中更常见的统计分析记号$X\beta=y$ 来替代$Ax=b$. 其中$X$为设计矩阵，$\beta$为参数向量，$y$为观测向量。

我们都知道身高和体重存在一定关系，但不是完美对应(数据集来自于R语言的women)

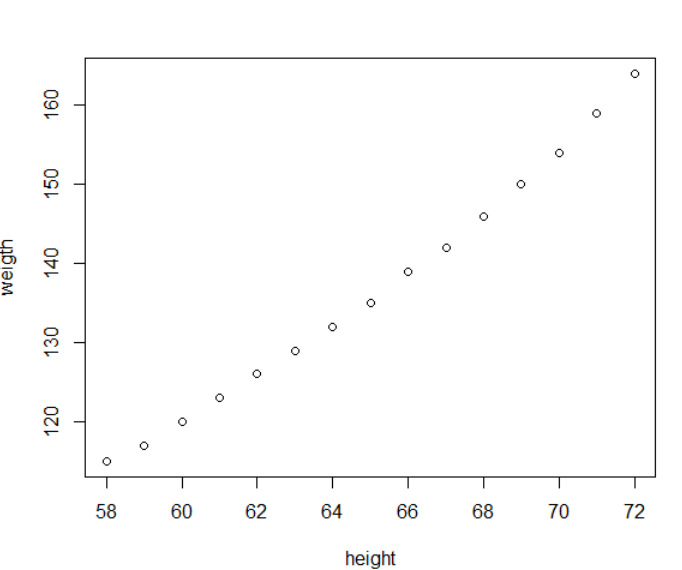
我们可以找到一条曲线去完美拟合已有的数据，但通常而言越复杂的模型就越容易出现过拟合的情况，不具有普适性，最好是找到一个简单模型，能对当前的数据做一个拟合，并且能预测未来。

两个变量最简单的关系就是线性方程$y=\beta_0 +\beta_1 x$。我们希望能够确定 $\beta_0$ 和 $\beta_1$使得预测值和观测值尽可能的接近，也就是让直线和数据尽可能的接近，最常用的度量方法就是余差平方之和最小。

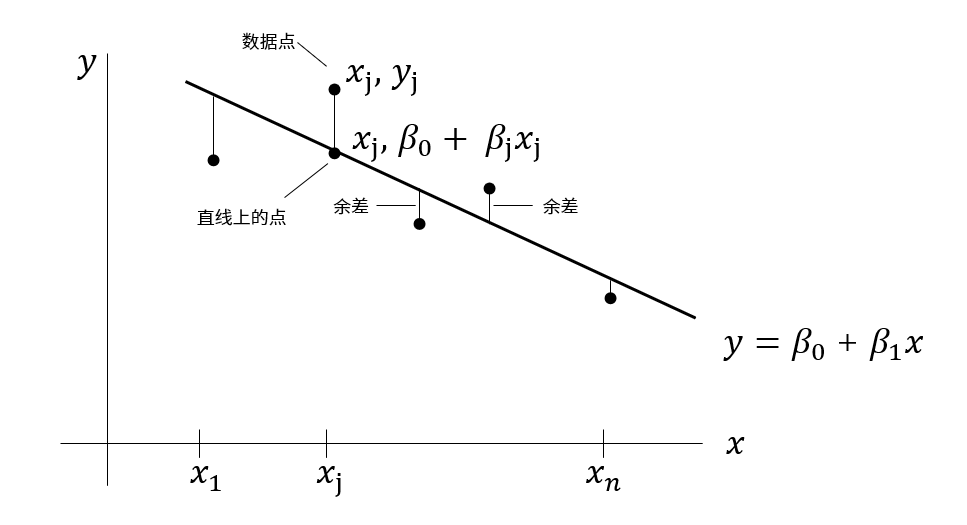
最小二乘直线$y=\beta_0 +\beta_1 x$是余差平方之和最小的，这条直线也被称之为y对x的回归直线。直线的系数 $ \beta_0$ 和 $\beta_1$称为线性回归系数。

如果数据点都落在直线上，那么参数 $ \beta_0$ 和 $\beta_1$满足如下方程，那么

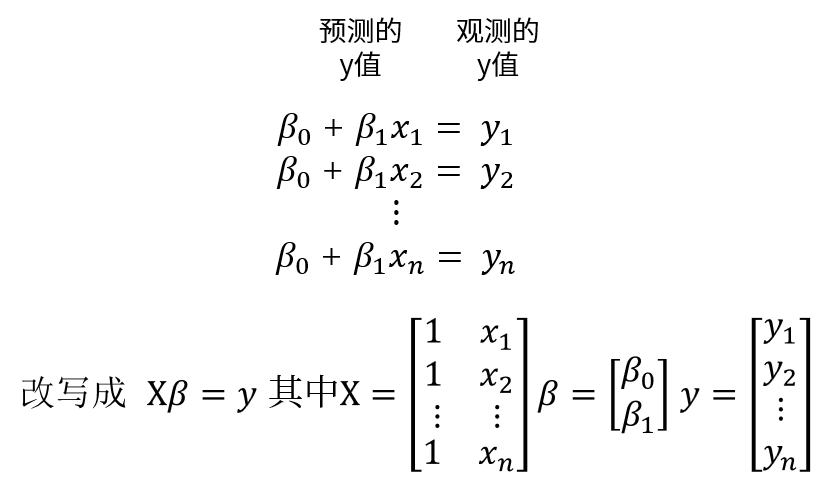
但是当数据点不在直线上时，这就意味着 $X\beta=y$ 没有解，那么问题其实是$Ax=b$的最小二乘问题，这两者仅仅记法不同。并且由于X的列线性无关，那么唯一的最小二乘解为$\hat \beta = R^{-1}Q^Ty$, 取$X=QR$，

接下来，我们就可以通过R语言的矩阵函数计算$\beta$

# 加载数据
data("women")

# 设置X和Y
X <- cbind(rep(1,length(women$height)), women$height)
y <- women$weight

# QR分解
qr <- qr(X)
Q <- qr.Q(qr)
R <- qr.R(qr) 
R.inv <- solve(R) # 求逆矩阵

# 计算
beta <- R.inv %*% t(Q) %*% y

根据求解结果，系数分别是-87.52和3.45, 我们来绘图展示下

plot(women$height, women$weight,
     xlab = "height", ylab="weigth")
x <- 58:72
y <- 3.45 * x - 87.52
lines(x=x,y=y)

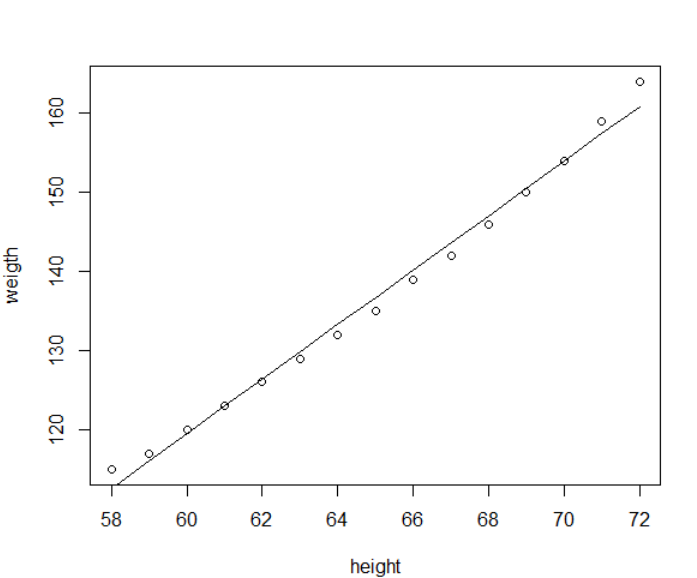
关于线性回归，R语言提供了lm函数，之前只是无脑调用，现在我把它的黑匣子打开了，它和我们之前做的事情类似，都有一步QR分解，只不过调用了不同的底层函数

# lm
z <- .Call(C_Cdqrls, ...
# qr
if(LAPACK)
     return(structure(.Internal(La_qr(x)), useLAPACK = TRUE, class = "qr"))
...           
res <- .Fortran(.F_dqrdc2,...

lm的输出信息有很多，比如说残差，系数的显著性水平，这些可以用summary.lm查看。

之前看「R语言实战」的回归章节时，总是不理解，看完就记住了几个函数而已。现在在线性代数理论基础上对这个部分有所理解了。

参考资料

如果对线性代数的最小二乘理论感兴趣，推荐阅读「线性代数及其应用」，戴维，原书第五版，第六章。

关于线性回归的R语言实现，推荐阅读「R语言实战」，第二版，第8章。

此外，维基百科的 最小二乘法页面也提供了比较好的解释。